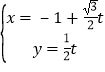题目内容
【题目】已知函数f(x)=cosx(sinx+cosx)﹣![]() .
.
(1)若0<α<![]() , 且sinα=
, 且sinα=![]() , 求f(α)的值;
, 求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
【答案】解:(1)∵0<α<![]() ,且sinα=
,且sinα=![]() ,
,
∴cosα=![]() ,
,
∴f(α)=cosα(sinα+cosα)﹣![]() ,
,
=![]() ×(
×(![]() +)﹣
+)﹣![]()
=![]() .
.
(2)f(x)=cosx(sinx+cosx)﹣![]() .
.
=sinxcosx+cos2x﹣![]()
=![]() sin2x+
sin2x+![]() cos2x
cos2x
=![]() sin(2x+
sin(2x+![]() ),
),
∴T=![]() =π,
=π,
由2kπ﹣![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,得kπ﹣
,k∈Z,得kπ﹣![]() ≤x≤kπ+
≤x≤kπ+![]() ,k∈Z,
,k∈Z,
∴f(x)的单调递增区间为[kπ﹣![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
【解析】(1)利用同角三角函数关系求得cosα的值,分别代入函数解析式即可求得f(α)的值.
(2)利用两角和公式和二倍角公式对函数解析式进行恒等变换,进而利用三角函数性质和周期公式求得函数最小正周期和单调增区间.

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,即
,即![]() .对上述数据作了初步处理,得到相关的值如下表:
.对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好.该公司某
内时认为该年效益良好.该公司某![]() 年投入的宣传费用(单位:万元)分别为:
年投入的宣传费用(单位:万元)分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试根据回归方程估计年销售量,从这
,试根据回归方程估计年销售量,从这![]() 年中任选
年中任选![]() 年,记其中选到效益良好年的数量为
年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.