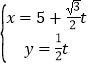题目内容
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合.直线l的参数方程为: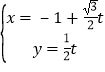 (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程,并指出C是什么曲线;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值。
【答案】解:(Ⅰ)∵ρ=4cosθ,∴ρ2=4ρcosθ,
由ρ2=x2+y2 , ρcosθ=x得:x2+y2=4x,
所以曲线C的直角坐标方程为(x﹣2)2+y2=4,
它是以(2,0)为圆心,半径为2的圆.
(Ⅱ)把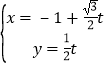 代入x2+y2=4x整理得
代入x2+y2=4x整理得![]() ,
,
设其两根分别为t1、t2 , 则![]() ,
,
∴![]()
【解析】(Ⅰ)由ρ=4cosθ可得ρ2=4ρcosθ,故曲线C的直角坐标方程为(x﹣2)2+y2=4,它是以(2,0)为圆心,半径为2的圆.
(Ⅱ)把参数方程代入x2+y2=4x整理得![]() , 利用根与系数的关系求得
, 利用根与系数的关系求得![]() , 根据
, 根据 ![]() 求得结果.
求得结果.
【考点精析】利用直线的参数方程对题目进行判断即可得到答案,需要熟知经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为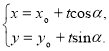 (
(![]() 为参数).
为参数).

练习册系列答案
相关题目
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)