题目内容
【题目】已知数列{an}前n项和Sn满足Sn+1=a2Sn+a1 , 其中a2≠0.
(Ⅰ)求证数列{an}是首项为1的等比数列;
(Ⅱ)当a2=2时,是否存在等差数列{bn},使得a1bn+a2bn﹣1+a3bn﹣2+…+anb1=2n+1﹣n﹣2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
【答案】证明:(Ⅰ)∵S1=a1 , ∴S2=a1+a2=a2a1+a1 ,
得:a2=a2a1 ,
∵a2≠0,
∴a1=1,
由Sn+1=a2Sn+a1可得:Sn+2=a2Sn+1+a1 , 减去前式,有an+2=a2an+1 ,
∴![]() ,
,
又![]() 也符合,
也符合,
故![]() 对n∈N*恒成立,数列{an}是首项为1,公比为a2的等比数列.
对n∈N*恒成立,数列{an}是首项为1,公比为a2的等比数列.
(Ⅱ)解:a2=2=q,a1=1,
∴![]() ,
,
设存在等差数列{bn}.则有:![]() ①
①![]() ②
②
将a1=1代入①,b1=1,
再结合a2=2代入②,b2=2,
故等差数列{bn}若存在,由b1=1、b2=2必有bn=n.
下面证明数列{bn}满足题意.
设Tn=a1bn+a2bn﹣1+a3bn﹣2+…+anb1=1×n+2×(n﹣1)+22×(n﹣2)+…+2n﹣2×2+2n﹣1×1 ③
则2Tn=2×n+22×(n﹣1)+23×(n﹣2)+…+2n﹣1×2+2n×1 ④,
④﹣③有:Tn=﹣n+2+22+…2n=2n+1﹣n﹣2,
∴存在等差数列{bn},bn=n使得a1bn+a2bn﹣1+a3bn﹣2+…+anb1=2n+1﹣n﹣2对一切n∈N*都成立
【解析】(Ⅰ)由S1=a1 , S2=a1+a2=a2a1+a1 , 可得a1=1,利用递推式Sn+1=a2Sn+a1 , Sn+2=a2Sn+1+a1 , 可得an+2=a2an+1 , 再利用等比数列的定义即可得出.
(II)a2=2=q,a1=1,可得:![]() , 设存在等差数列{bn}.则有:
, 设存在等差数列{bn}.则有:![]() ,
, ![]() , 可得b1=1,b2=2,故等差数列{bn}若存在,由b1=1、b2=2必有bn=n.再利用“错位相减法”、等比数列的前n项和公式即可得出.
, 可得b1=1,b2=2,故等差数列{bn}若存在,由b1=1、b2=2必有bn=n.再利用“错位相减法”、等比数列的前n项和公式即可得出.
【考点精析】掌握等比关系的确定和数列的前n项和是解答本题的根本,需要知道等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系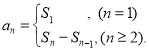 .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)