��Ŀ����
����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������![]() ����λ����Ԫ������������
����λ����Ԫ������������![]() ����λ���֣���������
����λ���֣���������![]() ����λ����Ԫ����Ӱ��.�Խ��������������
����λ����Ԫ����Ӱ��.�Խ��������������![]() ����������
����������![]() ���������˳���ͳ�ƣ��õ��������ݣ�
���������˳���ͳ�ƣ��õ��������ݣ�
��� | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
�������� | 38 | 48 | 58 | 68 | 78 | 88 |
�������� | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
������ģ�⣬������������![]() ����Ԫ������������
����Ԫ������������![]() ���֣�֮����������ϵʽ
���֣�֮����������ϵʽ![]() ����
����![]() .�������������˳����������õ���ص�ֵ���±���
.�������������˳����������õ���ص�ֵ���±���
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
��1�������������ݣ���![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��2���涨����Ʒ����������![]() ���֣�����������
���֣�����������![]() ����Ԫ���ı�ֵ������
����Ԫ���ı�ֵ������![]() ��ʱ��Ϊ����Ч������.�ù�˾ij
��ʱ��Ϊ����Ч������.�ù�˾ij![]() ��Ͷ����������ã���λ����Ԫ���ֱ�Ϊ��
��Ͷ����������ã���λ����Ԫ���ֱ�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���Ը��ݻع鷽�̹�����������������
���Ը��ݻع鷽�̹�����������������![]() ������ѡ
������ѡ![]() �꣬������ѡ��Ч�������������Ϊ
�꣬������ѡ��Ч�������������Ϊ![]() �������������
�������������![]() �ķֲ��к�����.������
�ķֲ��к�����.������![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����![]() ��
��
��������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() �е�б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
�е�б�ʺͽؾ����С���˹��Ʒֱ�Ϊ ��
��![]() .
.
���𰸡���1��![]() ��2��������
��2��������
����������������1�������⣬��![]() ��
��![]() ��������Իع鷽�̼��㹫ʽ�ɵ����е����Իع鷽��Ϊ
��������Իع鷽�̼��㹫ʽ�ɵ����е����Իع鷽��Ϊ![]() .
.
��2��������ɵã�![]() ��������������Ч������������
��������������Ч������������![]() ���ɳ����ηֲ��ɵ���ֲ��У�������ѧ����Ϊ
���ɳ����ηֲ��ɵ���ֲ��У�������ѧ����Ϊ![]() .
.
��⣺��1����![]() ��
��![]() ����ȡ������
����ȡ������![]() ����
����![]() ��
��![]()
��![]() ����������ݣ��ã�
����������ݣ��ã�![]() ��
��![]() ��
��
![]() ��
��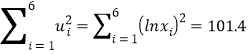 ��������
��������
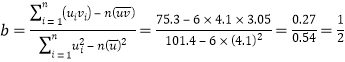 ��
��
![]() ����
����![]() ��
��
������ع鷽��Ϊ![]() .
.
��2����![]() ������
������![]() ����
����![]() ��������������������������
��������������������������
![]() �������
�������![]() ��
��![]() ��
��
![]() ��
��![]()
����![]() �ķֲ��������ʾ��
�ķֲ��������ʾ��
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��![]() .
.


