题目内容
3.解方程3sin2x+2sinxcosx-cos2x=0.分析 方程两边同除以cos2x,转化为以tanx为变量的一元二次方程,进行求解即可.
解答 解:显然cosx≠0…(1分),
方程两边同除以cos2x,得3tan2x+2tanx-1=0…(1分)
解得tanx=-1或tanx=$\frac{1}{3}$…(2分)
∴x=kπ-$\frac{π}{4}$或x=kπ+arctan$\frac{1}{3}$,k∈Z…(2分)
点评 本题主要考查三角方程的求解,根据条件转化为关于tanx的一元二次函数形式是解决本题的关键.

练习册系列答案
相关题目
13.函数y=$\frac{1}{\sqrt{x-1}}$的定义域是( )
| A. | [1,+∞) | B. | (1,+∞) | C. | (1,2) | D. | (-1,+∞) |
14.已知实数a,b,则“2a>2b”是“log2a>log2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.函数f(x)=tan(x+$\frac{π}{4}$)的单调递增区间为(以下的k∈Z)( )
| A. | (kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$) | B. | (kπ,(k+1)π) | C. | (kπ-$\frac{π}{4}$,kπ+$\frac{3π}{4}$) | D. | (kπ-$\frac{3π}{4}$,kπ+$\frac{π}{4}$) |
15.如果方程x2+(m-1)x+m2-2=0的两个实根一个小于-1,另一个大于1,那么实数m的取值范围是( )
| A. | -$\sqrt{2}$<m<$\sqrt{2}$ | B. | -2<m<0 | C. | -2<m<1 | D. | 0<m<1 |
13.若全集U=R,集合M={x|lg(x-1)<0},则∁UM为( )
| A. | [2,+∞) | B. | (-∞,1]∪[2,+∞) | C. | (2,+∞) | D. | (-∞,1)∪(2,+∞) |
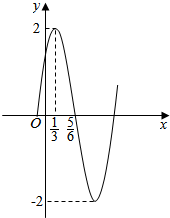 已知函数f(x)=Asin(ωx+ϕ)(A>0,?>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为y=2sin(πx+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+ϕ)(A>0,?>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为y=2sin(πx+$\frac{π}{6}$).