题目内容
13．若全集U=R，集合M={x|lg（x-1）＜0}，则∁UM为（ ）| A． | [2，+∞） | B． | （-∞，1]∪[2，+∞） | C． | （2，+∞） | D． | （-∞，1）∪（2，+∞） |
分析 先求出集合M的x范围，从而求出其补集．
解答 解：集合M={x|lg（x-1）＜0}={x|0＜x-1＜1}={x|1＜x＜2}，
∴则∁UM=（-∞，1]∪[2，+∞}，
故选：B．
点评 本题考查了集合的补集的定义及运算，考查对数函数的性质，是一道基础题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
4．a=${∫}_{0}^{2}$xdx，b=${∫}_{0}^{2}$exdx，c=${∫}_{0}^{2}$sinxdx，则a、b、c大小关系是（ ）
| A． | a＜c＜b | B． | a＜b＜c | C． | c＜b＜a | D． | c＜a＜b |
1．已知函数f（x）=Acos2（ωx+φ）+1（A＞0，ω＞0）的最大值为3，f（x）的图象在y轴上的截距为2，其相邻两对称轴间的距离为1，则f（1）+f（2）+f（3）+…+f（100）=（ ）
| A． | 0 | B． | 100 | C． | 150 | D． | 200 |
2．定义在R上的函数f（x）满足$f（x）=\left\{{\begin{array}{l}{{{log}_3}（9-x），x≤0}\\{f（x-1），x＞0}\end{array}}\right.$，则f（3）的值为（ ）
| A． | 1 | B． | 2 | C． | -2 | D． | -3 |
3．
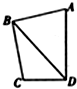已知一颗小米粒等可能地落入如图所示的平面四边形 ABCD（AD=$\frac{3}{2}$CD）内的任意一个位置，如果通过大量的试验发现米粒落入△BCD内的频率稳定在$\frac{2}{5}$附近，记点 B到直线 AD的距离与点 B到直线CD的距离的比值为λ，则函数f（x）=cos2x+2λsinx的最大值与最小值之和为（ ）
已知一颗小米粒等可能地落入如图所示的平面四边形 ABCD（AD=$\frac{3}{2}$CD）内的任意一个位置，如果通过大量的试验发现米粒落入△BCD内的频率稳定在$\frac{2}{5}$附近，记点 B到直线 AD的距离与点 B到直线CD的距离的比值为λ，则函数f（x）=cos2x+2λsinx的最大值与最小值之和为（ ）| A． | $-\frac{3}{2}$ | B． | $-\sqrt{2}$ | C． | $\frac{3}{2}$ | D． | $\sqrt{2}$ |