题目内容
15.已知函数f(x)=2x-(a+2)lnx-$\frac{a}{x}$.(1)当a=0时,求函数f(x)在x=1处的切线方程;
(2)当a>0时,求函数f(x)的极值.
分析 (1)欲求在点x=1处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.
(II)先求出f(x)的导数,分类讨论,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,再求出极值即可
解答 解:(1)当a=0时,f(x)=2x-2lnx$\frac{a}{x}$.
∴f′(x)=2-$\frac{2}{x}$.
函数函数f(x)在x=1处的切线斜率为f′(1)=0,
又f(1)=2,
故切线的方程为y-2=0,即y=2.
(2)函数f(x)的定义域为(0,+∞),
∴f′(x)=2-$\frac{a+2}{x}$+$\frac{a}{{x}^{2}}$=$\frac{(2x-a)(x-1)}{{x}^{2}}$
令f′(x)=0,得x=1或x=$\frac{1}{2}$a,
①当0<$\frac{a}{2}$<1,即0<a<2时,由f′(x)<0,得到x∈($\frac{a}{2}$,1),
由f′(x)>0,得到x∈(0,$\frac{a}{2}$)∪(1+∞),
即f(x)的单调增区间是∈(0,$\frac{a}{2}$),(1+∞),单调减区间是($\frac{a}{2}$,1),
所以,f(x)的极大值为f($\frac{a}{2}$)=a-(a+2)ln$\frac{a}{2}$-2,
极小值为f(1)=2-a.
②当$\frac{a}{2}$>1,即a>2时,由f′(x)<0,得到x∈(1,$\frac{a}{2}$),
由f′(x)>0,得到x∈(0,1)∪($\frac{a}{2}$,+∞),
即f(x)的单调增区间是∈(0,1),($\frac{a}{2}$,+∞),单调减区间是(1,$\frac{a}{2}$),
所以,f(x)的极大值为f(1)=2-a,
极小值为f($\frac{a}{2}$)=a-(a+2)ln$\frac{a}{2}$-2,
③当a=2时,f′(x)≥0,故f(x)在(0,+∞)单调递增,
所以此时f(x)没有极值.
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力及分类讨论思想.属于中档题.

| 年龄 | 23 | 27 | 39 | 41 | 45 | 49 | 50 | 53 | 56 | 58 | 60 |
| 脂肪 | 9.5 | 17.8 | 21.2 | 25.9 | 27.5 | 26.3 | 28.2 | 29.6 | 31.4 | 33.5 | 35.2 |
| A. | 某人年龄37岁,他体内脂肪含量为20.90% | |
| B. | 某人年龄37岁,他体内脂肪含量为20.90%的概率最大 | |
| C. | 某人年龄37岁,他体内脂肪含量的期望值为20.90% | |
| D. | 20.90%是对年龄为37岁的人群中的大部分人的体内脂肪含量所作出的估计 |
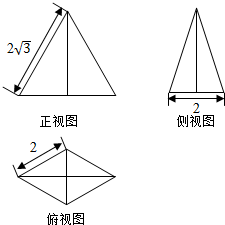 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 2 |
| A. | {x|-2≤x<4} | B. | {x|x≤2} | C. | {x|x>-4} | D. | {x|x≤2或x>4} |