题目内容
10.在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:| 年龄 | 23 | 27 | 39 | 41 | 45 | 49 | 50 | 53 | 56 | 58 | 60 |
| 脂肪 | 9.5 | 17.8 | 21.2 | 25.9 | 27.5 | 26.3 | 28.2 | 29.6 | 31.4 | 33.5 | 35.2 |
| A. | 某人年龄37岁,他体内脂肪含量为20.90% | |
| B. | 某人年龄37岁,他体内脂肪含量为20.90%的概率最大 | |
| C. | 某人年龄37岁,他体内脂肪含量的期望值为20.90% | |
| D. | 20.90%是对年龄为37岁的人群中的大部分人的体内脂肪含量所作出的估计 |
分析 由回归分析的几何意义可知:x=37时,y的预报值为20.901,即20.90%是对年龄为37岁的人群中的大部分人的体内脂肪含量所作出的估计.
解答 解:利用回归方程为$\stackrel{∧}{y}$=0.577x-0.448,
可得x=37时,$\stackrel{∧}{y}$=20.901,
即我们到年龄37岁时体内脂肪含量约为20.90%,
故20.90%是对年龄为37岁的人群中的大部分人的体内脂肪含量所作出的估计,
故选:D.
点评 本题考查的知识点是线性回归方程,熟练掌握并正确理解回归分析的实际意义,是解答的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
20. 已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )
已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )
 已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )
已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )| A. | (2,11) | B. | (3,10) | C. | (4,9) | D. | (5,8) |
1.设f(x)=2|x|,则${∫}_{-2}^{4}$f(x)dx=( )
| A. | $\frac{12}{ln2}$ | B. | $\frac{20}{ln2}$ | C. | $\frac{18}{ln2}$ | D. | $\frac{16}{ln2}$ |
19.对于向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$和实数λ,下列判断正确的是( )
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 若λ$\overrightarrow{a}$=0,则λ=0 | C. | 若$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ | D. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$ |
20.下列各组函数f(x)与g(x)的图象相同的是( )
| A. | f(x)=(x-1)0与g(x)=1 | B. | f(x)=x与g(x)=$\sqrt{x^2}$ | ||
| C. | f(x)=$\frac{{{x^2}-4}}{x-2}$,g(x)=x+2 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}x(x≥0)\\-x(x<0)\end{array}$ |
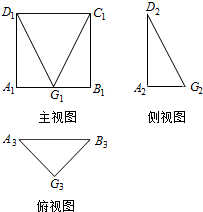 一个空间几何体G-ABCD的三视图如图所示,其中Ai,Bi,Ci,Di,Gi(i=1,2,3)分别是A,B,C,D五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形A1B1C1D1为正方形且A1B1=2a;在左视图中A2D2⊥A2G2,俯视图中A3G3=B3G3,
一个空间几何体G-ABCD的三视图如图所示,其中Ai,Bi,Ci,Di,Gi(i=1,2,3)分别是A,B,C,D五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形A1B1C1D1为正方形且A1B1=2a;在左视图中A2D2⊥A2G2,俯视图中A3G3=B3G3,