题目内容
20.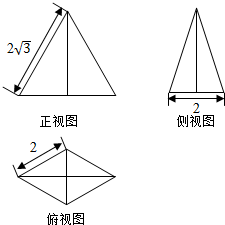 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 2 |
分析 根据已知中的三视图及相关视图边的长度,我们易判断出该几何体的形状及底面积和高的值,代入棱锥体积公式即可求出答案.
解答 解:由已知中该几何中的三视图中有两个三角形一个菱形可得:
这个几何体是一个四棱锥,
由图可知,底面两条对角线的长分别为2$\sqrt{3}$,2,底面边长为2,
故底面棱形的面积为$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$,
侧棱为2$\sqrt{3}$,
则棱锥的高h=$\sqrt{(2\sqrt{3})^{2}-{\sqrt{3}}^{2}}$=3,
故V=$\frac{1}{3}$•3•2$\sqrt{3}$=2 $\sqrt{3}$,
故选:A.
点评 本题考查的知识点是由三视图求面积、体积其中根据已知求出满足条件的几何体的形状及底面面积和棱锥的高是解答本题的关键

练习册系列答案
相关题目
 某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?
某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?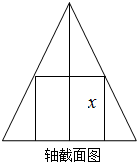 一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱:
一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱: