题目内容
(1)在平面直角坐标系xOy中,点P到两点(0,-
),(0,
)的距离之和等于4,设点P的轨迹为C.求出C的方程及其离心率e的大小;
(2)已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线x-y+2
=0的距离为3.求椭圆的方程.
| 3 |
| 3 |
(2)已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线x-y+2
| 2 |
考点:椭圆的简单性质,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)根据已知条件及椭圆的定义即知,点P的轨迹为以(0,-
),(0,
)为焦点,长半轴长为2的椭圆,所以得到对半轴长为1,所以C的方程为x2+
=1,并且可求得离心率e=
;
(2)可设椭圆方程为
+
=1,并且可得b=1,右焦点为(c,0),而根据点到直线的距离公式即可求出c=
,所以得到a2=3,所以所求椭圆方程便是
+y2=1.
| 3 |
| 3 |
| y2 |
| 4 |
| ||
| 2 |
(2)可设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| x2 |
| 3 |
解答:
解:(1)设P(x,y),由椭圆定义可知,点P的轨迹C是以(0,-
),(0,
)为焦点,长半轴长为2的椭圆;
它的短半轴长b=
=1;
故曲线C的方程为x2+
=1;
a=2,c=
,所以离心率e=
=
;
(2)设所求椭圆方程为
+
=1(a>b>0);
依题意有,b=1;
右焦点(c,0)到直线x-y+2
=0的距离为3;
∴
=3,解得c=
或c=-4
(舍去);
∴a2=b2+c2=1+2=3;
∴所求椭圆方程为
+y2=1.
| 3 |
| 3 |
它的短半轴长b=
22-(
|
故曲线C的方程为x2+
| y2 |
| 4 |
a=2,c=
| 3 |
| c |
| a |
| ||
| 2 |
(2)设所求椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
依题意有,b=1;
右焦点(c,0)到直线x-y+2
| 2 |
∴
|c-0+2
| ||
|
| 2 |
| 2 |
∴a2=b2+c2=1+2=3;
∴所求椭圆方程为
| x2 |
| 3 |
点评:考查椭圆的定义,以及椭圆的标准方程,椭圆的离心率的定义,以及椭圆的顶点,点到直线的距离公式及a2=b2+c2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
| 1+2sin500°cos500° |
| A、sin40°-cos40° |
| B、cos40°-sin40° |
| C、sin40°+cos40° |
| D、sin40°•cos40° |
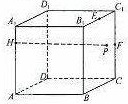 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )| A、9 | ||
B、27--6
| ||
C、51-14
| ||
D、14-3
|