题目内容

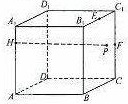如图，已知正方体ABCD-A1B1C1D1的棱长为4，点H在棱AA1上，且HA1=1，点E、F分别为B1C1、CC1的中点，P为侧面BCC1B1上一动点，且PE⊥PF，则当点P运动时，求HP2的最小值是（　　）
A、9
B、27--6
2
C、51-14
2
D、14-3
2
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：首先根据题意建立等量关系进一步求出最小值．
解答： 解：以EF为直径在平面BCC1B1内做圆，该圆的半径为
2
，再过H引BB1的垂线，垂足为G，连接GP，
所以：HP2=HG2+GP2，其中HG为棱长等于4，因此当GP最小时，HP就取最小值：3-
2

所以：HP2=(3-
2
)2+42=27-6
2

则：HP2的最小值27-6
2

故选：B
点评：本题考查的知识要点：空间点间的距离的应用．属于中等题型．
练习册系列答案
相关题目
复数
3-2i
(1+i)2
（i为虚数单位）的虚部为
 
．
已知函数f（x）=
3x，x≥0
x2，x＜0
，则f（f（-2））=
 
．
函数f（x）=
2x-2，x∈[1，+∞)
x2-2x，x∈(-∞，1)
，则函数y=f（x）-
1
4
的零点是
 
．
（1）在平面直角坐标系xOy中，点P到两点(0，-
3
)，(0，
3
)的距离之和等于4，设点P的轨迹为C．求出C的方程及其离心率e的大小；
（2）已知椭圆的一个顶点为A（0，-1），焦点在x轴上．若右焦点到直线x-y+2
2
=0的距离为3．求椭圆的方程．
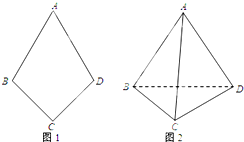如图1，平面四边形ABCD关于直线AC对称，∠A=60°，∠C=
90°，CD=2，把△ABD沿BD折起（如图2），使二面角A-BD-C为直二面角．如图2，
（Ⅰ）求AD与平面ABC所成的角的余弦值；
（Ⅱ）求二面角B-AC-D的大小的正弦值．
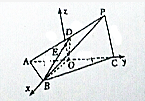如图，在三棱锥P-ABC中，△ABC是正三角形，∠PCA=90°，D是PA的中点，二面角P-AC-B为120°，PC=2，AB=2
3
，取AC的中点O为坐标原点建立空间直角坐标系，如图所示，BD交z轴于点E．
（1）求B、D、P三点的坐标；
（2）求BD与地面ABC所成角的余弦值．
若x，y满足约束条件
5x+y≥5
x+y≤4
y-ex≥0
，则
y
x
的取值范围是
 
．
已知函数f（x）=
x3，x∈(-2，2)
2x，x∈(2，π)
cosx，x∈(π，2π)
，求f（x）在区间（-2，2π）上的定积分．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网