题目内容
给出下面的四个命题:
①函数y=|sin(2x+
)|的最小正周期是
;
②函数y=sin(x-
)在区间[π,
]上单调递增;
③x=
是函数y=sin(2x+
)的图象的一条对称轴.
④函数f(x)=2sin(ωx)在[-
,
]上是增函数,ω可以是1或2.
其中正确的命题是 .
①函数y=|sin(2x+
| π |
| 3 |
| π |
| 2 |
②函数y=sin(x-
| 3π |
| 2 |
| 3π |
| 2 |
③x=
| 5π |
| 4 |
| 5π |
| 2 |
④函数f(x)=2sin(ωx)在[-
| π |
| 3 |
| π |
| 4 |
其中正确的命题是
考点:命题的真假判断与应用
专题:三角函数的图像与性质
分析:①,利用y=sinx的周期为2π,y=|sinx|的最小正周期是π(周期减半),从而可判断①;
②,利用诱导公式可得函数y=sin(x-
)=cosx,利用余弦函数的单调性质可判断②;
③,当x=
时,函数y=sin(2×
+
)=sin5π=0≠±1,可判断③.
④,当ω=1或ω=22时,分别判断函数f(x)=2sin(ωx)在[-
,
]上的单调性,可判断④.
②,利用诱导公式可得函数y=sin(x-
| 3π |
| 2 |
③,当x=
| 5π |
| 4 |
| 5π |
| 4 |
| 5π |
| 2 |
④,当ω=1或ω=22时,分别判断函数f(x)=2sin(ωx)在[-
| π |
| 3 |
| π |
| 4 |
解答:
解:①,∵y=|sinx|的最小正周期是π,是y=sinx的周期的一半,
∴函数y=|sin(2x+
)|的最小正周期是
,即①正确;
②,∵y=sin(x-
)=cosx,在区间[π,
]上单调递增,故②正确;
③,∵当x=
时,y=sin(2×
+
)=sin5π=0≠±1,
∴x=
不是函数y=sin(2x+
)的图象的一条对称轴,故③错误;
④,当ω=1时,f(x)=2sinx在[-
,
]上是增函数,
当ω=2时,x∈[-
,
]⇒2x∈[-
,
]
f(x)=2sin2x在[-
,
]不是增函数,
虽然ω=2时,不符合题意,但ω=1时,符号题意,
所以函数f(x)=2sin(ωx)在[-
,
]上是增函数,ω可以是1或2,正确;
故答案为:①②④.
∴函数y=|sin(2x+
| π |
| 3 |
| π |
| 2 |
②,∵y=sin(x-
| 3π |
| 2 |
| 3π |
| 2 |
③,∵当x=
| 5π |
| 4 |
| 5π |
| 4 |
| 5π |
| 2 |
∴x=
| 5π |
| 4 |
| 5π |
| 2 |
④,当ω=1时,f(x)=2sinx在[-
| π |
| 3 |
| π |
| 4 |
当ω=2时,x∈[-
| π |
| 3 |
| π |
| 4 |
| 2π |
| 3 |
| π |
| 2 |
f(x)=2sin2x在[-
| π |
| 3 |
| π |
| 4 |
虽然ω=2时,不符合题意,但ω=1时,符号题意,
所以函数f(x)=2sin(ωx)在[-
| π |
| 3 |
| π |
| 4 |
故答案为:①②④.
点评:本题考查三角函数的图象与性质,着重考查正弦函数的周期性、对称性、单调性的分析与判断,考查等价转化思想与运算求解能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若A(-1,1)和圆C(x-5)2+(y-7)2=4,一束光线从A点经过X轴反射到圆周C的最短路程是( )
| A、-10 | ||
B、6
| ||
C、4
| ||
| D、8 |
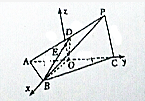 如图,在三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D是PA的中点,二面角P-AC-B为120°,PC=2,AB=2
如图,在三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D是PA的中点,二面角P-AC-B为120°,PC=2,AB=2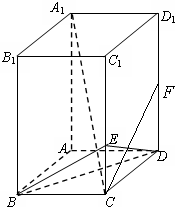 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,BB1=4,E是棱CC1上的点,且CE=1;F是DD1中点
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,BB1=4,E是棱CC1上的点,且CE=1;F是DD1中点