题目内容
| 1+2sin500°cos500° |
| A、sin40°-cos40° |
| B、cos40°-sin40° |
| C、sin40°+cos40° |
| D、sin40°•cos40° |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：直接利用同角三角函数的基本关系式，以及诱导公式化简求解即可．
解答：
解：
=
=
=
=cos40°-sin40°．
故选：B．
| 1+2sin500°cos500° |
=
| (sin500°+cos500°)2 |
=
| (sin140°+cos140°)2 |
=
| (sin40°-cos40°)2 |
=cos40°-sin40°．
故选：B．
点评：本题考查同角三角函数的基本关系式的应用，三角函数值的符号，基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
若A（-1，1）和圆C（x-5）2+（y-7）2=4，一束光线从A点经过X轴反射到圆周C的最短路程是（ ）
| A、-10 | ||
B、6
| ||
C、4
| ||
| D、8 |
集合M={y|y=x2-1}，N={y|y=3-x2}，则M∩N等于（ ）
| A、{y|-1≤y≤3} |
| B、{（-1，2），（1，2）} |
| C、∅ |
| D、R |
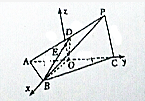如图，在三棱锥P-ABC中，△ABC是正三角形，∠PCA=90°，D是PA的中点，二面角P-AC-B为120°，PC=2，AB=2