题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据已知条件及正弦定理求得![]() ,即可知
,即可知![]() ,即
,即![]() ,再由
,再由![]() ,可证明
,可证明![]() 平面
平面![]() ,进而由平面与平面垂直的判定定理证明平面
,进而由平面与平面垂直的判定定理证明平面![]() 平面
平面![]() ;
;
(2)作![]() ,连接
,连接![]() ,根据线段关系可求得
,根据线段关系可求得![]() 的三边长,由余弦定理求得
的三边长,由余弦定理求得![]() ,进而由同角三角函数关系式求得
,进而由同角三角函数关系式求得![]() ,即可求得
,即可求得![]() .根据等体积法,即可求得点
.根据等体积法,即可求得点![]() 到平面
到平面![]() 的距离
的距离![]() ,即可由线面夹角的求法求得直线
,即可由线面夹角的求法求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明: 四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由正弦定理可得![]() ,代入可得
,代入可得![]()
所以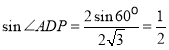
所以![]()
则![]()
所以![]()
因为四棱锥![]() 中,
中,![]() 平面
平面![]()
所以![]() ,且
,且![]()
所以![]() 平面
平面![]()
由因为![]() 平面
平面![]()
由平面与平面垂直的判定定理可得平面![]() 平面
平面![]()
(2)作![]() ,连接
,连接![]() ,如下图所示:
,如下图所示:
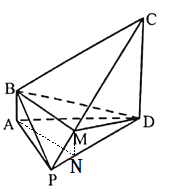
在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]()
由![]() ,可知
,可知![]()
由![]() 平面
平面![]() ,
,![]() 可得
可得![]() 平面
平面![]()
因为![]() ,所以
,所以![]() 平面
平面![]()
可得![]()
所以![]() ,则四边形
,则四边形![]() 为矩形.
为矩形.
![]()
所以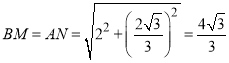 ,
,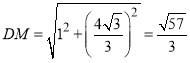
由(1)可得![]()
由![]() 平面
平面![]() ,可得
,可得![]()
所以![]()
则在![]() 中,
中,![]() ,
,![]() ,
,![]()
由余弦定理可知![]()
代入可得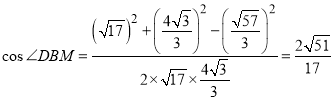
所以由同角三角函数关系式可得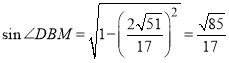
所以![]()
设点![]() 到平面
到平面![]() 的距离为
的距离为![]()
由![]()
则![]()
所以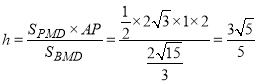
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]()
则直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值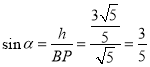

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,统计结果如下表所示,已知这100位顾客中一次购物量超过7件的顾客占![]() .
.
一次购物量 | 1至3件 | 4至7件 | 8至11件 | 12至15件 | 16件及以上 |
顾客数(人) |
| 27 | 20 |
| 10 |
结算时间( | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)确定![]() ,
,![]() 的值,并求顾客一次购物的结算时间的平均值;
的值,并求顾客一次购物的结算时间的平均值;
(2)从收集的结算时间不超过![]() 的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为
的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为![]() 的概率.(注:将频率视为概率)
的概率.(注:将频率视为概率)

