题目内容
在数列{an}中,an+1+an=2n-44(n∈N*),a1=-23.
(1)求an;
(2)设Sn为{an}的前n项和,求Sn的最小值.
(1)求an;
(2)设Sn为{an}的前n项和,求Sn的最小值.
(1)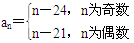
(2)-243
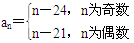
(2)-243
解:(1)∵an+1+an=2n-44,an+2+an+1=2(n+1)-44,
∴an+2-an=2.
∴a2+a1=-42,a1=-23,∴a2=-19.
同理得a3=-21,a4=-17,
故a1,a3,a5,…是以a1为首项、2为公差的等差数列,
a2,a4,a6,…是以a2为首项、2为公差的等差数列,
从而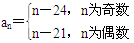 .
.
(2)当n为偶数时,Sn=(a1+a2)+(a3+a4)+…+(an-1+an)=(2×1-44)+(2×3-44)+(2×5-44)+…+[2×(n-1)-44]=2[1+3+…+(n-1)]-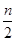 ·44=
·44=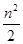 -22n,
-22n,
故当n=22时,Sn取得最小值-242.
当n为奇数时,Sn=a1+(a2+a3)+(a4+a5)+…+(an-1+an)=a1+(2×2-44)+(2×4-44)+…+[2×(n-1)-44]=a1+2[2+4+…+(n-1)]+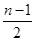 ·(-44)=-23+
·(-44)=-23+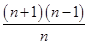 -22(n-1)=
-22(n-1)=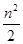 -22n-
-22n-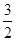 ,
,
故当n=21或n=23时,Sn取得最小值-243.
综上所述,Sn的最小值为-243.
∴an+2-an=2.
∴a2+a1=-42,a1=-23,∴a2=-19.
同理得a3=-21,a4=-17,
故a1,a3,a5,…是以a1为首项、2为公差的等差数列,
a2,a4,a6,…是以a2为首项、2为公差的等差数列,
从而
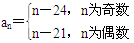 .
.(2)当n为偶数时,Sn=(a1+a2)+(a3+a4)+…+(an-1+an)=(2×1-44)+(2×3-44)+(2×5-44)+…+[2×(n-1)-44]=2[1+3+…+(n-1)]-
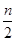 ·44=
·44=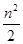 -22n,
-22n,故当n=22时,Sn取得最小值-242.
当n为奇数时,Sn=a1+(a2+a3)+(a4+a5)+…+(an-1+an)=a1+(2×2-44)+(2×4-44)+…+[2×(n-1)-44]=a1+2[2+4+…+(n-1)]+
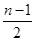 ·(-44)=-23+
·(-44)=-23+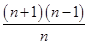 -22(n-1)=
-22(n-1)=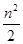 -22n-
-22n-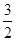 ,
,故当n=21或n=23时,Sn取得最小值-243.
综上所述,Sn的最小值为-243.

练习册系列答案
相关题目
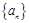 满足:
满足: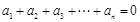 且
且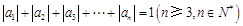 ,则称数列
,则称数列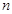 阶“归化数列”.
阶“归化数列”.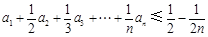 .
. (i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如
(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如 =8,则
=8,则 为 。
为 。
 的公差是2,若
的公差是2,若 成等比数列,则
成等比数列,则 项和
项和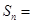 ( )
( )



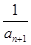 +
+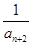 +
+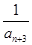 +…+
+…+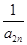 ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+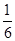 >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围. <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________.
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________. 满足
满足 ,
, ,且
,且 ,则
,则 .
.