题目内容
如果数列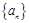 满足:
满足: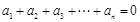 且
且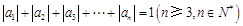 ,则称数列
,则称数列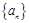 为
为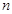 阶“归化数列”.
阶“归化数列”.
(1)若某4阶“归化数列”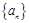 是等比数列,写出该数列的各项;
是等比数列,写出该数列的各项;
(2)若某11阶“归化数列”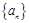 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;
(3)若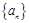 为n阶“归化数列”,求证:
为n阶“归化数列”,求证: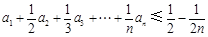 .
.
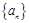 满足:
满足: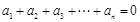 且
且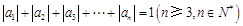 ,则称数列
,则称数列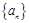 为
为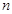 阶“归化数列”.
阶“归化数列”.(1)若某4阶“归化数列”
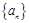 是等比数列,写出该数列的各项;
是等比数列,写出该数列的各项;(2)若某11阶“归化数列”
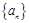 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;(3)若
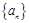 为n阶“归化数列”,求证:
为n阶“归化数列”,求证: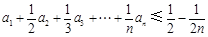 .
.(1)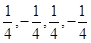 或
或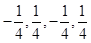 ;(2)
;(2) 或
或 ;(3)证明见解析.
;(3)证明见解析.
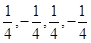 或
或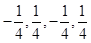 ;(2)
;(2) 或
或 ;(3)证明见解析.
;(3)证明见解析.试题分析:(1)等比数列
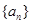 是4阶“归化数列”,则有
是4阶“归化数列”,则有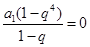 ,这样
,这样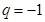 ,于是
,于是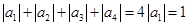 ,从而
,从而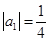 ,
,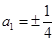 ,以后各项依次可写出;(2)等差数列
,以后各项依次可写出;(2)等差数列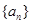 是11阶“归化数列”,则
是11阶“归化数列”,则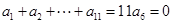 ,
,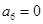 ,这样有
,这样有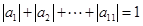 ,知当
,知当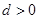 时,
时,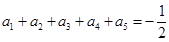 ,当
,当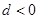 时,
时,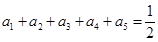 ,由此可得
,由此可得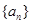 的通项公式分别为
的通项公式分别为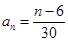 或
或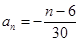 ;(3)对
;(3)对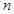 阶“归化数列”,从已知上我们只能知道在
阶“归化数列”,从已知上我们只能知道在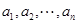 中有正有负,因此为了求
中有正有负,因此为了求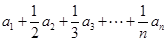 ,我们可以设
,我们可以设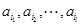 是正的,
是正的,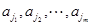 是负的,这样
是负的,这样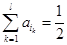 ,
,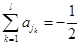 ,
,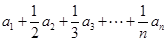
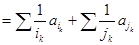
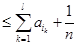
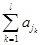
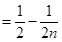
证毕.
(1)设
 成公比为
成公比为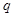 的等比数列,显然
的等比数列,显然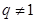 ,则由
,则由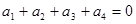 ,
,得
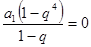 ,解得
,解得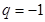 ,由
,由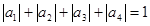 得
得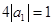 ,解得
,解得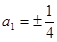 ,
,所以数列
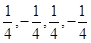 或
或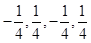 为所求四阶“归化数列”; 4分
为所求四阶“归化数列”; 4分(2)设等差数列
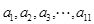 的公差为
的公差为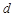 ,由
,由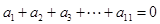 ,
,所以
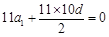 ,所以
,所以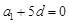 ,即
,即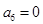 , 6分
, 6分当
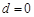 时,与归化数列的条件相矛盾,
时,与归化数列的条件相矛盾,当
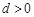 时,由
时,由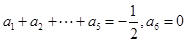 ,所以
,所以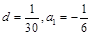 ,
,所以
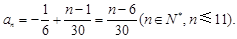 8分
8分当
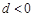 时,由
时,由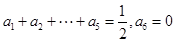 ,所以
,所以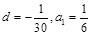 ,
,所以
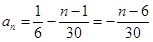 (n∈N*,n≤11),
(n∈N*,n≤11),所以
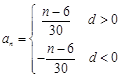 (n∈N*,n≤11), 10分
(n∈N*,n≤11), 10分(3)由已知可知,必有ai>0,也必有aj<0(i,j∈{1,2, ,n,且i≠j).
设
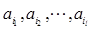 为诸ai中所有大于0的数,
为诸ai中所有大于0的数,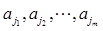 为诸ai中所有小于0的数.
为诸ai中所有小于0的数.由已知得X=
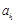 +
+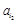 + +
+ +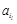 =
=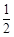 ,Y=
,Y= 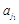 +
+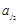 + +
+ +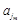 =-
=-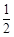 .
.所以
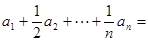
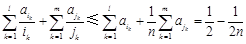 . 16分
. 16分 项和公式,不等式的放缩法.
项和公式,不等式的放缩法.
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
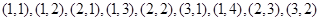 ,
,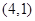 , ,则第60个数对是 .
, ,则第60个数对是 .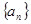 的各项均为正数,且
的各项均为正数,且
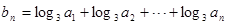 ,求数列
,求数列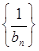 的前n项和
的前n项和 ;
;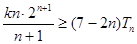 恒成立的实数
恒成立的实数 的取值范围.
的取值范围. 满足
满足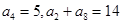 ,数列
,数列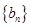 满足
满足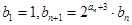 。
。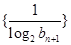 的前
的前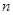 项和;
项和;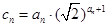 ,求数列
,求数列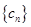 的前
的前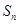
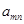 表示位于从上到下第
表示位于从上到下第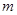 行,从左到右
行,从左到右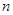 列的数,比如
列的数,比如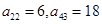 ,若
,若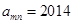 ,则有( )
,则有( )


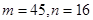

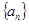 的前
的前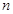 项和是
项和是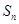 ,若
,若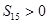 ,
,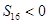 ,则
,则



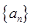 ,定义数列
,定义数列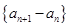 为数列
为数列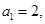
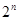 ,则数列
,则数列 .
.