题目内容
已知数列{an}中,a1=2,an-an-1-2n=0(n≥2,n∈N*).
(1)写出a2,a3的值(只写结果),并求出数列{an}的通项公式;
(2)设bn=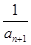 +
+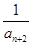 +
+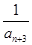 +…+
+…+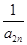 ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+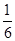 >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围.
(1)写出a2,a3的值(只写结果),并求出数列{an}的通项公式;
(2)设bn=
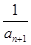 +
+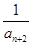 +
+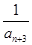 +…+
+…+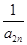 ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+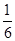 >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围.(1)a2=6,a3=12. an=n(n+1).
(2)实数t的取值范围为(-∞,-2)∪(2,+∞)
(2)实数t的取值范围为(-∞,-2)∪(2,+∞)
解:(1)∵a1=2,an-an-1-2n=0(n≥2,n∈N*),
∴a2=6,a3=12.
当n≥3时,an-an-1=2n,an-1-an-2=2(n-1),
又a3-a2=2×3,a2-a1=2×2,
∴an-a1=2[n+(n-1)+…+3+2],
∴an=2[n+(n-1)+…+3+2+1]=2×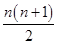 =n(n+1).
=n(n+1).
当n=1时,a1=2;当n=2时,a2=6,也满足上式,
∴数列{an}的通项公式为an=n(n+1).
(2)bn=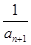 +
+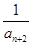 +…+
+…+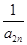
=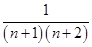 +
+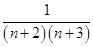 +…+
+…+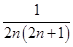
=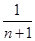 -
-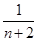 +
+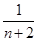 -
-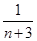 +…+
+…+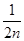 -
-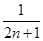
=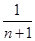 -
-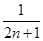
=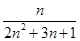
=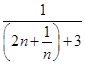 .
.
令f(x)=2x+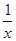 (x≥1),则f′(x)=2-
(x≥1),则f′(x)=2-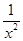 ,
,
当x≥1时,f′(x)>0恒成立,
∴函数f(x)在[1,+∞)上是增函数,
故当x=1时,f(x)min=f(1)=3,
即当n=1时,(bn)max=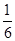 .
.
要使对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+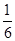 >bn恒成立,则需t2-2mt+
>bn恒成立,则需t2-2mt+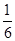 >(bn)max=
>(bn)max=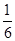 ,
,
即t2-2mt>0对?m∈[-1,1]恒成立,
∴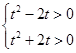 ,解得t>2或t<-2,
,解得t>2或t<-2,
∴实数t的取值范围为(-∞,-2)∪(2,+∞).
∴a2=6,a3=12.
当n≥3时,an-an-1=2n,an-1-an-2=2(n-1),
又a3-a2=2×3,a2-a1=2×2,
∴an-a1=2[n+(n-1)+…+3+2],
∴an=2[n+(n-1)+…+3+2+1]=2×
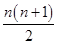 =n(n+1).
=n(n+1).当n=1时,a1=2;当n=2时,a2=6,也满足上式,
∴数列{an}的通项公式为an=n(n+1).
(2)bn=
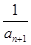 +
+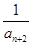 +…+
+…+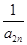
=
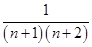 +
+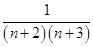 +…+
+…+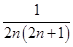
=
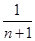 -
-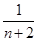 +
+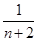 -
-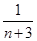 +…+
+…+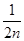 -
-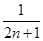
=
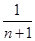 -
-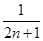
=
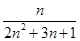
=
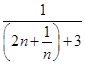 .
.令f(x)=2x+
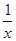 (x≥1),则f′(x)=2-
(x≥1),则f′(x)=2-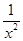 ,
,当x≥1时,f′(x)>0恒成立,
∴函数f(x)在[1,+∞)上是增函数,
故当x=1时,f(x)min=f(1)=3,
即当n=1时,(bn)max=
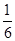 .
.要使对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
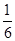 >bn恒成立,则需t2-2mt+
>bn恒成立,则需t2-2mt+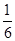 >(bn)max=
>(bn)max=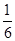 ,
,即t2-2mt>0对?m∈[-1,1]恒成立,
∴
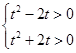 ,解得t>2或t<-2,
,解得t>2或t<-2,∴实数t的取值范围为(-∞,-2)∪(2,+∞).

练习册系列答案
相关题目
 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示 项和.
项和. 及
及 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求 .
. ,记
,记 ,
, ,其中
,其中 表示
表示 和
和 两个数中最大的数.
两个数中最大的数. ,求
,求 的值;
的值; 为
为 ,
, ,
, ,
, 四个数中最小的数,对于由两个数对
四个数中最小的数,对于由两个数对 组成的数对序列
组成的数对序列 和
和 ,试分别对
,试分别对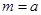 和
和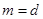 两种情况比较
两种情况比较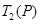 和
和 的大小;
的大小; 组成的所有数对序列中,写出一个数对序列
组成的所有数对序列中,写出一个数对序列 使
使 最小,并写出
最小,并写出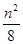 +
+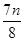
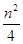 +
+
 +
+
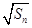 +
+ (n≥2),则数列{an}的通项公式为an=( )
(n≥2),则数列{an}的通项公式为an=( ) 满足
满足 ,若
,若 ,则
,则 =( )
=( )



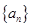 满足
满足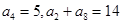 ,数列
,数列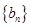 满足
满足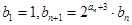 。
。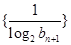 的前
的前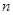 项和;
项和;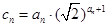 ,求数列
,求数列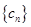 的前
的前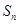
 是等差数列,首项
是等差数列,首项 ,则使前n项和
,则使前n项和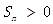 成立的最大自然数n是_______.
成立的最大自然数n是_______.