题目内容
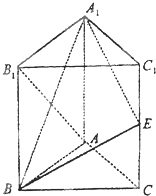
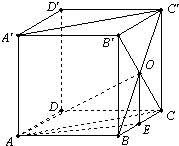
如图,正方体的棱长为1,B′C∩BC′=O,求:
(1)AO与A′C′所成角;
(2)AO与平面ABCD所成角的正切值;
(3)平面AOB与平面AOC所成角.

(1)AO与A′C′所成角;
(2)AO与平面ABCD所成角的正切值;
(3)平面AOB与平面AOC所成角.

(1)∵A′C′∥AC,∴AO与A′C′所成角就是∠OAC.∵OC⊥OB,AB⊥平面BC′,∴OC⊥OA,
在Rt△AOC中,OC═OC=
,AC=
,∴∠OAC=30°.(4分)
(2)如图,作OE⊥BC于E,连接AE,∵平面BC′⊥平面ABCD,∴OE⊥平面ABCD,∠OAE为OA与平面ABCD所成角.
在Rt△OAE中,OE=
,AE=
=
,∴tan∠OAE=
=
.(9分)
(3)∵OC⊥OA,OC⊥OB,∴OC⊥平面AOB.又∵OC?平面AOC,∴平面AOB⊥平面AOC,即平面AOB与平面AOC所成角为90°.(13分)
在Rt△AOC中,OC═OC=
| ||
| 2 |
| 2 |
(2)如图,作OE⊥BC于E,连接AE,∵平面BC′⊥平面ABCD,∴OE⊥平面ABCD,∠OAE为OA与平面ABCD所成角.
在Rt△OAE中,OE=
| 1 |
| 2 |
12+(
|
| ||
| 2 |
| OE |
| AE |
| ||
| 5 |
(3)∵OC⊥OA,OC⊥OB,∴OC⊥平面AOB.又∵OC?平面AOC,∴平面AOB⊥平面AOC,即平面AOB与平面AOC所成角为90°.(13分)


练习册系列答案
相关题目