题目内容
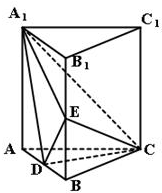
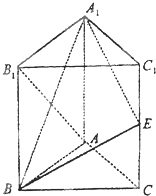
如图,正三棱柱ABC-A1B1C1的各棱长都为m,E是侧棱CC1的中点,求证AB1⊥平面A1BE.

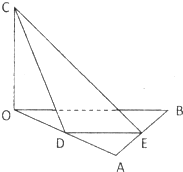
证明:取BC的中点O作为坐标原点.
建立如图所示的空间直角坐标系,不妨设m=2.
则A(-
,0,0),B(0,-1,0),B1(0,-1,2),A1(-
,0,2),E(0,1,1).
∴
=(
,-1,2),
=(0,2,1),
=(-
,1,2).
∴
•
=0-2+2=0,
•
=-3-1+4=0.
∴
⊥
,
⊥
,即AB1⊥BE,AB1⊥BA1.
又∵BE∩BA1=B.
∴AB1⊥平面A1BE.
建立如图所示的空间直角坐标系,不妨设m=2.

则A(-
| 3 |
| 3 |
∴
| AB1 |
| 3 |
| BE |
| BA1 |
| 3 |
∴
| AB1 |
| BE |
| AB1 |
| BA1 |
∴
| AB1 |
| BE |
| AB1 |
| BA1 |
又∵BE∩BA1=B.
∴AB1⊥平面A1BE.

练习册系列答案
相关题目