题目内容
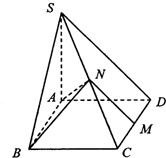
如图,已知四棱锥S-ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,SA=AD=1,AB=
.
(I)求证:MN⊥平面ABN;
(II)求二面角A-BN-C的余弦值.
| 2 |
(I)求证:MN⊥平面ABN;
(II)求二面角A-BN-C的余弦值.

(I)证明:以A点为原点,AB为x轴,AD为y轴,AZ为z轴的空间直角坐标系,
如图所示.则依题意可知相关各点的坐标分别是:A(0,0,0),B(
,0,0),
C(
,1,0),D(0,1,0),S(0,0,1),
∴M(
,1,0),N(
,
,
).(2分)
∴
=(0,-
,
),
=(
,0,0),
=(
,
,
).(4分)
∴
•
═0,
•
═0.∴
⊥
,
⊥
.
∴MN⊥平面ABN.(7分)
(II)设平面NBC的法向量
=(a,b,c),则
⊥
,
⊥
.
且又易知
=(0,1,0),
=(
,1,-1)
∴
即
∴
令a=1,则
=(1,0,
).(11分)
显然,
=(0,-
,
)就是平面ABN的法向量.
∴cos<
,
>=
═
.
由图形知,二面角A-BN-C是钝角二面角(12分)
∴二面角A-BN-C的余弦值是-
.(14分)
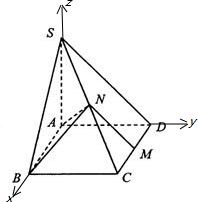
如图所示.则依题意可知相关各点的坐标分别是:A(0,0,0),B(
| 2 |
C(
| 2 |
∴M(
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| 2 |
| AN |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| MN |
| AB |
| MN |
| AN |
| MN |
| AB |
| MN |
| AN |
∴MN⊥平面ABN.(7分)
(II)设平面NBC的法向量
| n |
| n |
| BC |
| n |
| SC |
且又易知
| BC |
| SC |
| 2 |
∴
|
|
|
令a=1,则
| n |
| 2 |
显然,
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
∴cos<
| n |
| MN |
| ||||
|
|
| ||
| 3 |
由图形知,二面角A-BN-C是钝角二面角(12分)
∴二面角A-BN-C的余弦值是-
| ||
| 3 |


练习册系列答案
相关题目