题目内容
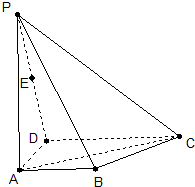
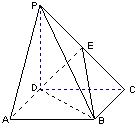
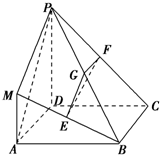
如图,已知三棱锥P-ABC的侧面PAB是等边三角形,D是AB的中点,PC=BC=AC=2,PB=2
.
(1)证明:AB⊥平面PCD;
(2)求点C到平面PAB的距离.
| 2 |
(1)证明:AB⊥平面PCD;
(2)求点C到平面PAB的距离.

证明:(1)∵BC=AC,△PAB是等边三角形,D是AB的中点,
∴CD⊥AB,PD⊥AB,
又PD∩CD=D,
∴AB⊥平面PCD.
(2)∵BC=AC=2,AB=PB=2
,
∴AC2+BC2=AB2,∴∠ACB=90°,
故△ACB是直角三角形,
∴S△ACB=
AC•BC=
×2×2=2,
∵PC=BC=AC=2,PB=2
.
∴PC2+BC2=PB2,∴∠PCB=90°,∴PC⊥BC.
∵△PAB是等边三角形,∴PA=2
.
同理可证PC⊥CA.
又AC∩CB=C,
∴PC⊥平面BAC.
∴PC是三棱锥P-ABC的高,
∴Vp-ABC=
S△ABC•PC=
×2×2=
又∵△PAB是边长为2
等边三角形,
∴S△ABP=
PA•PBsin60°=
×(2
)2×
=2
,
设点C到平面PAB的距离为h,则VC-PAB=
S△PAB•h=
h,
∵VC-PAB=VP-ABC,即
h=
,解得h=
.
∴点C到平面PAB的距离为
.
∴CD⊥AB,PD⊥AB,
又PD∩CD=D,
∴AB⊥平面PCD.
(2)∵BC=AC=2,AB=PB=2
| 2 |
∴AC2+BC2=AB2,∴∠ACB=90°,
故△ACB是直角三角形,
∴S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∵PC=BC=AC=2,PB=2
| 2 |
∴PC2+BC2=PB2,∴∠PCB=90°,∴PC⊥BC.
∵△PAB是等边三角形,∴PA=2
| 2 |
同理可证PC⊥CA.
又AC∩CB=C,
∴PC⊥平面BAC.
∴PC是三棱锥P-ABC的高,
∴Vp-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
又∵△PAB是边长为2
| 2 |
∴S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
设点C到平面PAB的距离为h,则VC-PAB=
| 1 |
| 3 |
2
| ||
| 3 |
∵VC-PAB=VP-ABC,即
2
| ||
| 3 |
| 4 |
| 3 |
2
| ||
| 3 |
∴点C到平面PAB的距离为
2
| ||
| 3 |

练习册系列答案
相关题目