题目内容
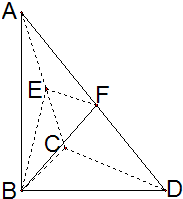
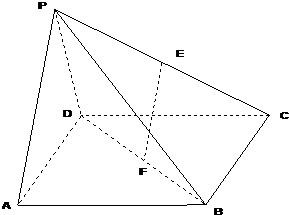
如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=CD=1,AB=
,E、F分别为AC、AD的中点.
(1)求证:平面BEF⊥平面ABC;
(2)求直线AD与平面BEF所成角的正弦值.
| 3 |
(1)求证:平面BEF⊥平面ABC;
(2)求直线AD与平面BEF所成角的正弦值.

(1)证明:∵AB⊥平面BCD,
∴AB⊥CD.
又∵CD⊥BC,
∴CD⊥平面ABC.
∵E、F分别为AC、AD的中点,
∴EF∥CD.
∴EF⊥平面ABC,
∵EF?平面BEF,
∴平面BEF⊥平面ABC.
(2)过A作AH⊥BE于H,连接HF,
由(1)可得AH⊥平面BEF,
∴∠AFH为直线AD与平面BEF所成角.
在Rt△ABC中,AB=
,BC=1,E为AC中点,
∴∠ABE=30°,
∴AH=
AB=
.
在Rt△BCD中,BC=CD=1,
∴BD=
.
∴在Rt△ABD中,AD=
∴AF=
AD=
.
∴在Rt△AFH中,sin∠AFH=
=
,
∴AD与平面BEF所成角的正弦值为
.
∴AB⊥CD.
又∵CD⊥BC,
∴CD⊥平面ABC.
∵E、F分别为AC、AD的中点,
∴EF∥CD.
∴EF⊥平面ABC,
∵EF?平面BEF,
∴平面BEF⊥平面ABC.
(2)过A作AH⊥BE于H,连接HF,
由(1)可得AH⊥平面BEF,
∴∠AFH为直线AD与平面BEF所成角.
在Rt△ABC中,AB=
| 3 |
∴∠ABE=30°,
∴AH=
| 1 |
| 2 |
| ||
| 2 |
在Rt△BCD中,BC=CD=1,
∴BD=
| 2 |
∴在Rt△ABD中,AD=
| 5 |
∴AF=
| 1 |
| 2 |
| ||
| 2 |
∴在Rt△AFH中,sin∠AFH=
| AH |
| AF |
| ||
| 5 |
∴AD与平面BEF所成角的正弦值为
| ||
| 5 |

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目



 y=0的距离是( )
y=0的距离是( )