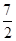题目内容
在区间[0，3]上任取三个数x，y，z，则使得不等式（x-1）2+y2+z2≤1成立的概率（ ）
A．
| B．
| C．
| D．
|
在区间[0，3]上任取三个数x，y，z，所有的点对应的区域为
位于空间坐标系中第一卦限的、棱长等于3的正方体，其体积为V=33=27
而满足不等式（x-1）2+y2+z2≤1的点，
位于以（1，0，0）为球心，半径为1的球面及其内部．
该球位于正方体内部的体积为V1=
×
=
因此，所求的概率为P=
=
故选：C
位于空间坐标系中第一卦限的、棱长等于3的正方体，其体积为V=33=27
而满足不等式（x-1）2+y2+z2≤1的点，
位于以（1，0，0）为球心，半径为1的球面及其内部．
该球位于正方体内部的体积为V1=
| 1 |
| 4 |
| 4π |
| 3 |
| π |
| 3 |
因此，所求的概率为P=
| V1 |
| V |
| π |
| 81 |
故选：C
练习册系列答案
高中必刷题系列答案
相关题目
y＝0的距离是( )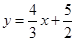
的距离为（ ）
