题目内容
3.(1)已知f(x)=m+$\frac{2}{{3}^{x}-1}$是奇函数,求常数m的值;(2)问k为何值时,方程|3x-1|=k无解,有一解,有两解?
分析 (1)由题意得f(x)+f(-x)=m+$\frac{2}{{3}^{x}-1}$+m+$\frac{2}{{3}^{-x}-1}$=0,从而解得;
(2)作函数y=|3x-1|的图象,从而结合图象写出方程的解的个数.
解答 解:(1)∵f(x)=m+$\frac{2}{{3}^{x}-1}$是奇函数,
∴f(x)+f(-x)=m+$\frac{2}{{3}^{x}-1}$+m+$\frac{2}{{3}^{-x}-1}$=0,
故m=-$\frac{1}{2}$($\frac{2}{{3}^{x}-1}$+$\frac{2}{{3}^{-x}-1}$)=1;
(2)作函数y=|3x-1|的图象如下,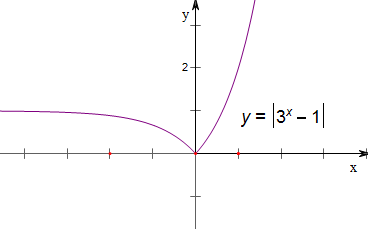
结合图象可知,
当k=0或k≥1时,方程有一个解,
当0<k<1时,方程有两个解,
当k<0时,方程没有解.
点评 本题考查了函数的性质的应用及数形结合的思想应用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
13.(1g2)3+(1g5)3+31g21g5的值是( )
| A. | 4 | B. | 1 | C. | 6 | D. | 3 |
13.区间(-∞,1)∪(1,+∞)可以作为以下哪个不等式的解集( )
| A. | x2-2x+1≤0 | B. | x2-2x+1≥0 | C. | x2-2x+1>0 | D. | x2-2x+1<0 |