题目内容
已知二次函数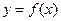 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为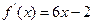 ,数列
,数列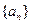 的前n项和为
的前n项和为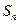 ,点
,点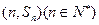 均在函数
均在函数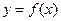 的图像上。(Ⅰ)求数列
的图像上。(Ⅰ)求数列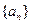 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设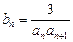 ,
,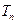 是数列
是数列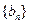 的前n项和,求使得
的前n项和,求使得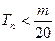 对所有
对所有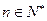 都成立的最小正整数m.
都成立的最小正整数m.
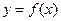 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为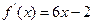 ,数列
,数列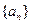 的前n项和为
的前n项和为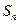 ,点
,点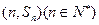 均在函数
均在函数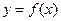 的图像上。(Ⅰ)求数列
的图像上。(Ⅰ)求数列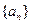 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设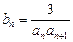 ,
,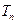 是数列
是数列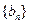 的前n项和,求使得
的前n项和,求使得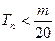 对所有
对所有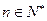 都成立的最小正整数m.
都成立的最小正整数m.解:(Ⅰ)设这二次函数f(x)=ax2+bx (a≠0) ,
则 f`(x)=2ax+b,由于f`(x)=6x-2,
得 a="3" , b=-2, 所以 f(x)=3x2-2x. ………3分
又因为点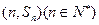 均在函数
均在函数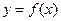 的图像上,所以
的图像上,所以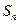 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-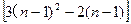 =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (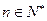 )
)
(Ⅱ)由(Ⅰ)得知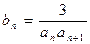 =
=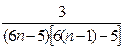 =
=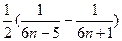
故Tn=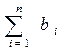 =
=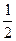
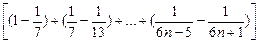 =
=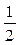 (1-
(1-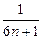 ).
).
因此,要使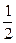 (1-
(1-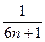 )﹤
)﹤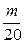 (
(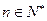 )成立的m,必须且仅须满足
)成立的m,必须且仅须满足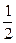 ≤
≤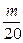 ,
,
即m≥10,所以满足要求的最小正整数m为10.
则 f`(x)=2ax+b,由于f`(x)=6x-2,
得 a="3" , b=-2, 所以 f(x)=3x2-2x. ………3分
又因为点
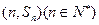 均在函数
均在函数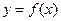 的图像上,所以
的图像上,所以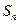 =3n2-2n.
=3n2-2n.当n≥2时,an=Sn-Sn-1=(3n2-2n)-
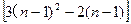 =6n-5.
=6n-5.当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (
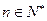 )
) (Ⅱ)由(Ⅰ)得知
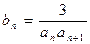 =
=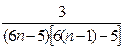 =
=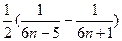
故Tn=
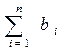 =
=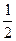
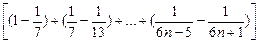 =
=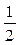 (1-
(1-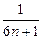 ).
).因此,要使
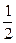 (1-
(1-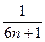 )﹤
)﹤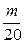 (
(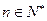 )成立的m,必须且仅须满足
)成立的m,必须且仅须满足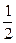 ≤
≤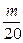 ,
,即m≥10,所以满足要求的最小正整数m为10.
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
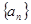 ,
,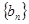 满足a1=2,2an=1+anan+1,bn=an-1, bn≠0
满足a1=2,2an=1+anan+1,bn=an-1, bn≠0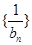 是等差数列,并求数列
是等差数列,并求数列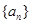 的通项公式;
的通项公式;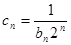 Tn为数列
Tn为数列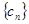 的前n项和,求证:Tn<2
的前n项和,求证:Tn<2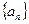 的前
的前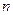 项和为
项和为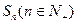 ,点
,点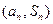 在直线
在直线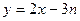 .
.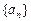 的通项公式;
的通项公式;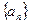 各项均为正数,
各项均为正数,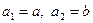 ,且对于正整数
,且对于正整数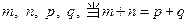 时,都有
时,都有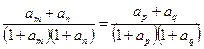 。
。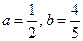 ,求
,求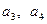 的值,并求数列
的值,并求数列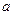 ,存在与
,存在与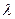 ,使得对于每个正整数
,使得对于每个正整数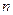 ,都有
,都有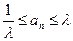 。
。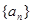 的公差为2,若
的公差为2,若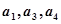 成等比数列,则
成等比数列,则
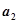 =( )
=( )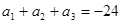 ,
,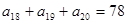 ,则此数列前20项和等于( )
,则此数列前20项和等于( )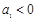 ,
,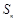 为第n项,且
为第n项,且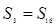 ,则
,则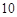
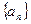 中,
中,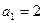 ,
,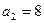 ,且已知函数
,且已知函数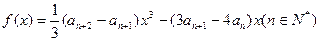 在
在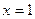 处取得极值。
处取得极值。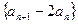 是等比数列
是等比数列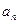 和前
和前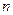 项和
项和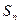
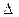 ABC中,a,b,c成等比数列,则cos(A-C)+cosB+cos2B=
ABC中,a,b,c成等比数列,则cos(A-C)+cosB+cos2B=