题目内容
已知圆 内一点
内一点 过点
过点 的直线
的直线 交圆
交圆 于
于 两点,且满足
两点,且满足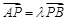 (
( 为参数).
为参数).
(1)若 ,求直线
,求直线 的方程;
的方程;
(2)若 求直线
求直线 的方程;
的方程;
(3)求实数 的取值范围.
的取值范围.
(1)  或
或 (2)
(2)  (3)
(3) 
解析试题分析:(1)当直线 的斜率不存在时,
的斜率不存在时,  ,不满足,故可设所求直线
,不满足,故可设所求直线 的方程为
的方程为 ,代入圆的方程,整理得
,代入圆的方程,整理得 ,利用弦长公式可求得直线方程为
,利用弦长公式可求得直线方程为 或
或 .
.
(2)当直线 的斜率不存在时,
的斜率不存在时,  或
或 ,不满足,故可设所求直线
,不满足,故可设所求直线 的方程为
的方程为 ,代入圆的方程,整理得
,代入圆的方程,整理得 ,(*)设
,(*)设 ,则
,则 为方程(*)的两根,由
为方程(*)的两根,由 可得
可得 ,则有
,则有 ,
, 得
得 ,解得
,解得 ,所以直线
,所以直线 的方程为
的方程为
(3)当直线 的斜率不存在时,
的斜率不存在时,  或
或 ,
, 或
或 ,当直线
,当直线 的斜率存在时可设所求直线
的斜率存在时可设所求直线 的方程为
的方程为 ,代入圆的方程,整理得
,代入圆的方程,整理得 ,(*)设
,(*)设 ,则
,则 为方程(*)的两根,由
为方程(*)的两根,由 可得
可得 ,则有
,则有 ,
, 得
得 ,而
,而 ,由
,由 可解得
可解得 ,所以实数
,所以实数 的取值范围为
的取值范围为 -
-
考点:本题考查了直线与圆的位置关系
点评:平面解析几何里解决直线与圆的位置关系有以下两种方法:一是联立直线和圆组成方程组,若方程组有两组解,则说明直线与圆相交;若只有一组解,则说明直线与圆相切;若无解,则直线与圆相离.二是看圆心到直线距离d与圆半径r大小,若d>r,则直线与圆相离;若d<r,则直线与圆相交;若d=r,则直线与圆相切.

练习册系列答案
相关题目
 的圆心与点
的圆心与点 关于直线
关于直线 对称,直线
对称,直线 与圆
与圆 、
、 两点,且
两点,且 ,求圆
,求圆 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 .
.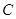 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆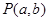 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,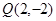 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 轴的交点为
轴的交点为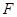 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 过点
过点 在极坐标系中的方程为
在极坐标系中的方程为 ,圆C在极坐标系中的方程为
,圆C在极坐标系中的方程为 ,求圆C被直线
,求圆C被直线 的圆的方程.
的圆的方程. ,B(
,B( ), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标.
), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标. 截直线
截直线 的弦长为
的弦长为 ;
; 的值;
的值;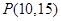 的圆的切线所在的直线方程.
的圆的切线所在的直线方程. 上,且经过圆
上,且经过圆 与圆
与圆 的交点的圆方程.
的交点的圆方程.