题目内容
若圆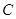 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆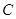 外一点
外一点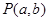 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,
(Ⅰ)求圆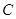 的方程;
的方程;
(Ⅱ)已知点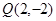 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 的方程;若不是,请说明理由;
的方程;若不是,请说明理由;
(Ⅲ)若(Ⅱ)中直线 与
与 轴的交点为
轴的交点为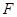 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 为直径的圆
为直径的圆 过点
过点 ,圆
,圆 是否过定点?证明你的结论.
是否过定点?证明你的结论.
(1)
(2)
(3)圆 过定点
过定点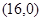 和
和
解析试题分析:解(Ⅰ)设圆心 由题易得
由题易得 1分 半径
1分 半径 , 2分
, 2分
得 ,
, 3分 所以圆
3分 所以圆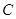 的方程为
的方程为 4分
4分
(Ⅱ)由题可得 5分 所以
5分 所以 -6分
-6分 7分
7分
所以
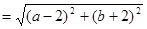 整理得
整理得
所以点 总在直线
总在直线 上 8分
上 8分
(Ⅲ) 9分 由题可设点
9分 由题可设点 ,
, ,
,
则圆心 ,半径
,半径 10分
10分
从而圆 的方程为
的方程为 11分
11分
整理得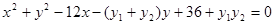 又点
又点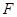 在圆
在圆 上,故
上,故
得 12分 所以
12分 所以
令 得
得 , 13分 所以
, 13分 所以 或
或
所以圆 过定点
过定点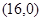 和
和 14分
14分
考点:圆的方程
点评:主要是考查了圆的方程以及直线方程的求解,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程.
)两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程. 轴正半轴上,直线
轴正半轴上,直线 与圆C相切
与圆C相切 的直线
的直线 与圆C交于不同的两点
与圆C交于不同的两点 且为
且为 时
时 的面积.
的面积. 轴正半轴上,直线
轴正半轴上,直线 与圆C相切
与圆C相切 的直线
的直线 与圆C交于不同的两点
与圆C交于不同的两点 且为
且为 时,求:
时,求: 的面积.
的面积. 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为,圆心在上.
的半径为,圆心在上.
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心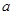 的取值范围.
的取值范围. 内一点
内一点 过点
过点 的直线
的直线 交圆
交圆 于
于 两点,且满足
两点,且满足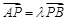 (
( 为参数).
为参数). ,求直线
,求直线 求直线
求直线 (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
 的最小值.
的最小值. 与两平行直线
与两平行直线 都相切,且圆心
都相切,且圆心 在直线
在直线 上,
上, 与
与 两点,
两点,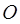 为坐标原点且满足
为坐标原点且满足 ,求直线
,求直线