题目内容
(本题满分10分)
求圆心在直线 上,且经过圆
上,且经过圆 与圆
与圆 的交点的圆方程.
的交点的圆方程.
(x+2)2 +(y+1)2 =17.
解析试题分析:先通过两圆方程联立求得交点AB坐标,再根据圆的几何性质可知圆心应线段AB的垂直平分线与直线x-y+1=0的交点,从而求得圆心坐标,再根据过点A,B求得半径,写出圆的标准方程.
设圆 与圆
与圆 的交点为A、B,解方程组:
的交点为A、B,解方程组: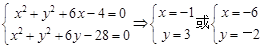 …………………………4分;
…………………………4分;
所以A(-1,3)、B(-6,-2)
因此直线AB的垂直平分线方程为:x+y+3=0…………………6分; 与x+y+3=0联立,解得:x=-2,y=-1,即:所求圆心C为(-2,-1)……8分;
与x+y+3=0联立,解得:x=-2,y=-1,即:所求圆心C为(-2,-1)……8分;
半径r=AC=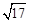 .
.
故所求圆C的方程为:(x+2)2 +(y+1)2 =17……………………………4分;.
考点:圆的标准方程及几何性质.
点评:求出两圆的交点坐标之后,关键是根据圆心是AB的垂直平分线与直线x-y+1=0的交点求出圆心坐标,从而求得圆的方程.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 内一点
内一点 过点
过点 的直线
的直线 交圆
交圆 于
于 两点,且满足
两点,且满足 (
( 为参数).
为参数). ,求直线
,求直线 求直线
求直线 与两平行直线
与两平行直线 都相切,且圆心
都相切,且圆心 在直线
在直线 上,
上, 与
与 两点,
两点, 为坐标原点且满足
为坐标原点且满足 ,求直线
,求直线 过点
过点 与圆
与圆 相切,
相切, :
: 的焦点为圆
的焦点为圆 的圆心,直线
的圆心,直线 与
与 交于不同的两点
交于不同的两点 .
. 。
。 过两点
过两点 ,且圆心
,且圆心 上.
上. 是直线
是直线 上的动点,
上的动点, 是圆
是圆 为切点,求四边形
为切点,求四边形 面积的最小值.
面积的最小值. 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
. 、
、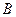 的坐标分别为
的坐标分别为 、
、
 ,动点
,动点 满足
满足 .
. 的方程;
的方程; 作直线与轨迹
作直线与轨迹 求切点的坐标.
求切点的坐标.