题目内容
设x=1与x=2是函数f(x)=alnx+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)试判断x=1,x=2是函数f(x)的极大值还是极小值,并说明理由.
(1)试确定常数a和b的值;
(2)试判断x=1,x=2是函数f(x)的极大值还是极小值,并说明理由.
(1) a=-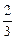 ,b=-
,b=-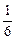 , (2) 在x=1处函数f(x)取得极小值
, (2) 在x=1处函数f(x)取得极小值 ,在x=2处函数取得极大值
,在x=2处函数取得极大值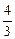 -
-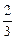 ln2
ln2
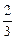 ,b=-
,b=-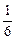 , (2) 在x=1处函数f(x)取得极小值
, (2) 在x=1处函数f(x)取得极小值 ,在x=2处函数取得极大值
,在x=2处函数取得极大值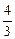 -
-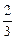 ln2
ln2 f′(x)= +2bx+1
+2bx+1
(1)由极值点的必要条件可知:f′(1)=f′(2)=0,
即a+2b+1=0,且 +4b+1=0,解方程组可得a=-
+4b+1=0,解方程组可得a=-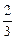 ,b=-
,b=-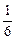 ,
,
∴f(x)=-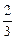 lnx-
lnx-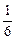 x2+x
x2+x
(2)f′(x)=-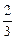 x-1-
x-1-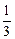 x+1,当x∈(0,1)时,f′(x)<0,
x+1,当x∈(0,1)时,f′(x)<0,
当x∈(1,2)时,f′(x)>0,
当x∈(2,+∞)时,f′(x)<0,
故在x=1处函数f(x)取得极小值 ,在x=2处函数取得极大值
,在x=2处函数取得极大值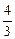 -
-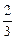 ln2.
ln2.
 +2bx+1
+2bx+1(1)由极值点的必要条件可知:f′(1)=f′(2)=0,
即a+2b+1=0,且
 +4b+1=0,解方程组可得a=-
+4b+1=0,解方程组可得a=-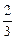 ,b=-
,b=-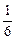 ,
,∴f(x)=-
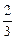 lnx-
lnx-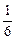 x2+x
x2+x(2)f′(x)=-
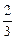 x-1-
x-1-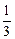 x+1,当x∈(0,1)时,f′(x)<0,
x+1,当x∈(0,1)时,f′(x)<0,当x∈(1,2)时,f′(x)>0,
当x∈(2,+∞)时,f′(x)<0,
故在x=1处函数f(x)取得极小值
 ,在x=2处函数取得极大值
,在x=2处函数取得极大值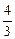 -
-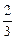 ln2.
ln2.
练习册系列答案
相关题目
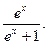
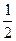 )对称;
)对称;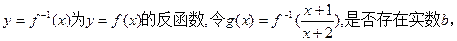 使得任给
使得任给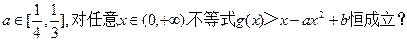 若存在,求b的取值范围;若不存在,说明理由.
若存在,求b的取值范围;若不存在,说明理由.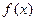 =
=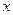 (1-
(1-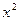 )在[0,1]上的最大值为__________.
)在[0,1]上的最大值为__________.

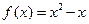 ,则
,则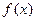 在区间
在区间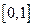 上的最大值为( )
上的最大值为( )


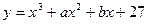 在
在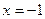 处有极大值,在
处有极大值,在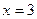 处极小值,则
处极小值,则 ,
,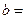
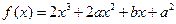 ,
,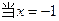 时有极值7,则
时有极值7,则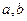 的值分别为 ;
的值分别为 ;