题目内容
已知函数f(x)=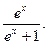
(Ⅰ)证明函数y=f(x)的图象关于点(0,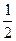 )对称;
)对称;
(Ⅱ)设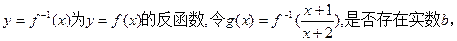 使得任给
使得任给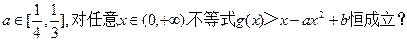 若存在,求b的取值范围;若不存在,说明理由.
若存在,求b的取值范围;若不存在,说明理由.
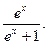
(Ⅰ)证明函数y=f(x)的图象关于点(0,
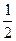 )对称;
)对称;(Ⅱ)设
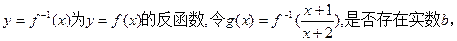 使得任给
使得任给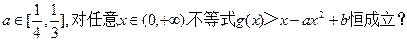 若存在,求b的取值范围;若不存在,说明理由.
若存在,求b的取值范围;若不存在,说明理由.(1)见解析(2)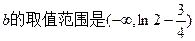
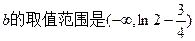
(Ⅰ)在y=f(x)的图象上任取一点P(x,y),它关于点(0,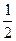 )对称的点为
)对称的点为
Q(-x,1-y)
由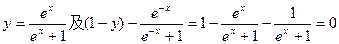
立知点Q在y=f(x)图象上.从而由P的任意性可知y=f(x)的图象关于点(0,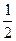 )对称.
)对称.
(Ⅱ)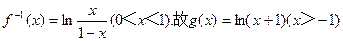
构造函数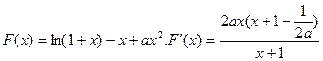
又x>0,a∈[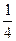 ,
,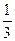 ]
]
若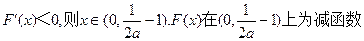 .
.
若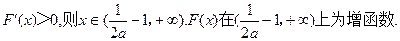
故当x>0时,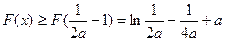
记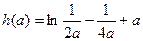
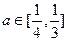
注意到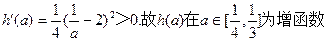
故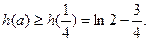 要使
要使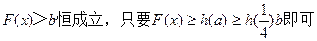
故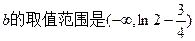
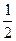 )对称的点为
)对称的点为Q(-x,1-y)
由
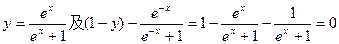
立知点Q在y=f(x)图象上.从而由P的任意性可知y=f(x)的图象关于点(0,
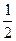 )对称.
)对称.(Ⅱ)
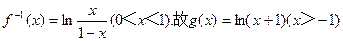
构造函数
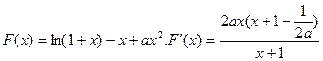
又x>0,a∈[
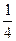 ,
,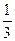 ]
]若
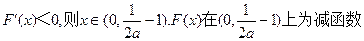 .
.若
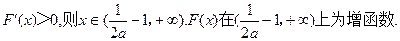
故当x>0时,
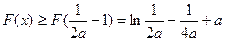
记
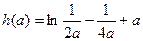
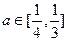
注意到
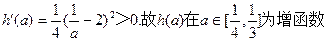
故
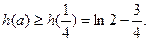 要使
要使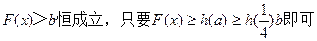
故
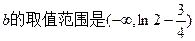

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 ,
,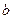 为实数)有极值,且在
为实数)有极值,且在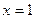 处的切线与直线
处的切线与直线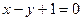 平行.
平行.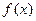 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;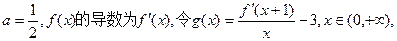
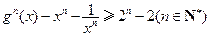 .
.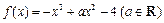 .
.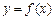 的图象在点P(1,
的图象在点P(1,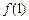 )处的切线的倾斜角为
)处的切线的倾斜角为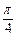 ,求实数a的值;
,求实数a的值;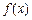 的导函数是
的导函数是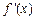 ,在 (1) 的条件下,若
,在 (1) 的条件下,若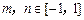 ,求
,求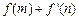 的最小值.
的最小值.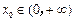 ,使
,使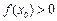 ,求a的取值范围.
,求a的取值范围.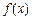 的导数
的导数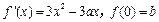 .a,b为实数,
.a,b为实数,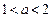 .
.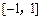 上的最小值、最大值分别为
上的最小值、最大值分别为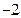 、1,求a、b的值;
、1,求a、b的值;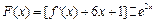 ,试判断函数
,试判断函数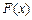 的极值点个数.
的极值点个数.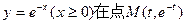 处的切线l与x轴、y轴所围成的三角形面积为S(t).
处的切线l与x轴、y轴所围成的三角形面积为S(t). 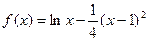 在[1,3]上的最大值和最小值.
在[1,3]上的最大值和最小值.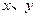 为正实数,且满足关系式
为正实数,且满足关系式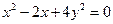 ,求
,求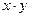 的最大值.
的最大值.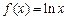 (Ⅰ)求函数
(Ⅰ)求函数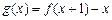 的最大值;(Ⅱ)当
的最大值;(Ⅱ)当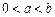 时,求证:
时,求证: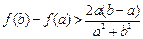 .
.