题目内容
求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.
当x=±2时,函数有最大值13,当x=±1时,函数有最小值4
先求导数,得y′=4x3-4x
令y′=0,即4x3-4x=0.
解得x1=-1,x2=0,x3=1.
导数y′的正负以及f(-2),f(2)如下表:
从上表知,当x=±2时,函数有最大值13,当x=±1时,函数有最小值4.
令y′=0,即4x3-4x=0.
解得x1=-1,x2=0,x3=1.
导数y′的正负以及f(-2),f(2)如下表:
| x | -2 | (-2,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,2) | 2 |
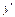 | | - | 0 | + | 0 | - | 0 | + | |
| y | 13 |  | 4 |  | 5 |  | 4 |  | 13 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
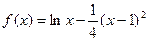 在[1,3]上的最大值和最小值.
在[1,3]上的最大值和最小值.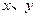 为正实数,且满足关系式
为正实数,且满足关系式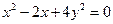 ,求
,求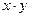 的最大值.
的最大值.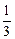 ,则
,则 在区间
在区间 上的最大值是
上的最大值是
 ,
, 的最大值和最小值。
的最大值和最小值。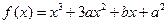 在
在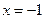 时有极值0,则
时有极值0,则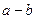 的值为 .
的值为 .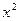 -
-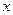 ,则
,则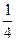 C
C  D
D