题目内容
函数y=2x4－4x3＋2x2在区间［0，2］上的最大值与最小值分别为
A．8， | B．，0 |
| C．8，0 | D．8，－ |
C
本题考查函数在给定闭区间上的最值.只需比较它的极值与端点值的大小即可.
y′=8x3－12x2＋4x,令y′=8x3－12x2＋4x=0,得x=0,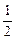
或1.
∵函数y=2x4－4x3＋2x2可导,
∴它在［0，2］上的极值点是x=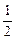,1.
∵f(0)=0,f()=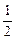
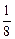,f(1)=0,f(2)=8,∴ymax=8,ymin=0.
y′=8x3－12x2＋4x,令y′=8x3－12x2＋4x=0,得x=0,
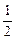或1.∵函数y=2x4－4x3＋2x2可导,
∴它在［0，2］上的极值点是x=
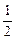,1.∵f(0)=0,f(
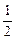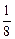)=,f(1)=0,f(2)=8,∴ymax=8,ymin=0.
练习册系列答案
相关题目
，
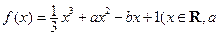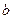为实数）有极值，且在
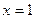处的切线与直线
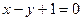平行.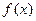
的极小值为1，若存在，求出实数a的值；若不存在，请说明理由；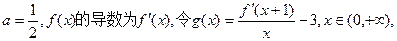
.
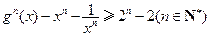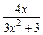,x∈［0，2］.
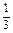ax3-a2x,x∈［0，2］.若对任意x1∈［0，2］，总存在x2∈［0，2］，使f(x1)-g(x2)=0.求实数a的取值范围.
有极大值又有极小值，则
的取值范围是 。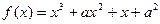
有两个极值点，则实数a的取值范围为 （ ）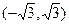
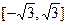
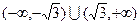
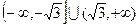
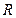上可导的函数
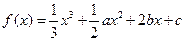，当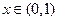
时取得极大值，当
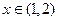时取得极小值，则
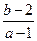的取值范围是 （ ）
