Question

【题目】如图，四棱锥P﹣ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．
（Ⅰ） 求证：PC⊥AD；
（Ⅱ） 在棱PB上是否存在一点Q，使得A，Q，M，D四点共面？若存在，指出点Q的位置并证明；若不存在，请说明理由；
（Ⅲ） 求点D到平面PAM的距离．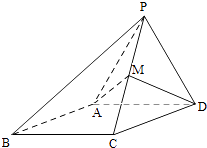

Answer 1

【答案】Ⅰ）证法一：取AD中点O，连结OP，OC，AC，
依题意可知△PAD，△ACD均为正三角形，
所以OC⊥AD，OP⊥AD，又OC∩OP=O，OC平面POC，OP平面POC，
所以AD⊥平面POC，又PC平面POC，
所以PC⊥AD．
证法二：连结AC，依题意可知△PAD，△ACD均为正三角形，
又M为PC的中点，所以AM⊥PC，DM⊥PC，
又AM∩DM=M，AM平面AMD，DM平面AMD，
所以PC⊥平面AMD，
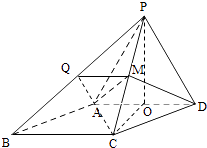
又AD平面AMD，所以PC⊥AD．（Ⅱ）解：当点Q为棱PB的中点时，A，Q，M，D四点共面，
证明如下：
取棱PB的中点Q，连结QM，QA，又M为PC的中点，所以QM∥BC，
在菱形ABCD中AD∥BC，所以QM∥AD，
所以A，Q，M，D四点共面．
（Ⅲ）解：点D到平面PAM的距离即点D到平面PAC的距离，
由（Ⅰ）可知PO⊥AD，又平面PAD⊥平面ABCD，
平面PAD∩平面ABCD=AD，PO平面PAD，
所以PO⊥平面ABCD，即PO为三棱锥P﹣ACD的体高．
在Rt△POC中， ， ，
在△PAC中，PA=AC=2， ，边PC上的高AM= ，
所以△PAC的面积 ，
设点D到平面PAC的距离为h，
由VD﹣PAC=VP﹣ACD得
，
又 ，
所以 ，
解得 ，
所以点D到平面PAM的距离为 ．

【解析】（Ⅰ）法一：取AD中点O，连结OP，OC，AC，依题意可知△PAD，△ACD均为正三角形，从而AD⊥平面POC，由此能证明PC⊥AD．
法二：连结AC，依题意可知△PAD，△ACD均为正三角形，从而AM⊥PC，DM⊥PC，由此能证明PC⊥AD．（Ⅱ）当点Q为棱PB的中点时，A，Q，M，D四点共面．取棱PB的中点Q，连结QM，QA，由已知得QM∥BC，由此能证明A，Q，M，D四点共面．（Ⅲ）点D到平面PAM的距离即点D到平面PAC的距离，由已知得得PO为三棱锥P﹣ACD的体高，由VD﹣PAC=VP﹣ACD ， 能求出点D到平面PAM的距离．
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点才能正确解答此题．