题目内容
【题目】已知函数f(x)=x2﹣x﹣ ![]() (x<0),g(x)=x2+bx﹣2(x>0),b∈R,若f(x)图象上存在A,B两个不同的点与g(x)图象上A′,B′两点关于y轴对称,则b的取值范围为( )
(x<0),g(x)=x2+bx﹣2(x>0),b∈R,若f(x)图象上存在A,B两个不同的点与g(x)图象上A′,B′两点关于y轴对称,则b的取值范围为( )
A.(﹣4 ![]() ﹣5,+∞)
﹣5,+∞)
B.(4 ![]() ﹣5,+∞)
﹣5,+∞)
C.(﹣4 ![]() ﹣5,1)
﹣5,1)
D.(4 ![]() ﹣5,1)
﹣5,1)
【答案】D
【解析】解:由题意知,方程f(﹣x)=g(x)在(0,+∞)上有两个不同的解,
即x2+x﹣ ![]() =x2+bx﹣2,
=x2+bx﹣2,
则b= ![]() +1﹣
+1﹣ ![]()
则b<1,
又b= ![]() ,
,
设h(x)= ![]() ,
,
则h′(x)= ![]() =
= ![]() ,
,
由h′(x)=0得x2﹣2x﹣1=0得x=1+ ![]() 或1﹣
或1﹣ ![]() (舍),
(舍),
当0<x<1+ ![]() 时,h′(x)<0,函数h(x)递减,
时,h′(x)<0,函数h(x)递减,
当x>1+ ![]() 时,h′(x)>0,函数h(x)递增,
时,h′(x)>0,函数h(x)递增,
则当x=1+ ![]() 时,h(x)取得极小值,
时,h(x)取得极小值,
此时h(1+ ![]() )=
)= ![]() +1﹣
+1﹣ ![]() =2(
=2( ![]() ﹣1)+1﹣
﹣1)+1﹣ ![]() =2
=2 ![]() ﹣2+1﹣
﹣2+1﹣ ![]() =2
=2 ![]() ﹣2+1﹣2(2﹣
﹣2+1﹣2(2﹣ ![]() )=4
)=4 ![]() ﹣5,
﹣5,
∴要使则b= ![]() +1﹣
+1﹣ ![]() 在(0,+∞)上有两个不同的交点,
在(0,+∞)上有两个不同的交点,
则4 ![]() ﹣5<b<1,
﹣5<b<1,
即a的取值范围是(4 ![]() ﹣5,1)
﹣5,1)
故选:D.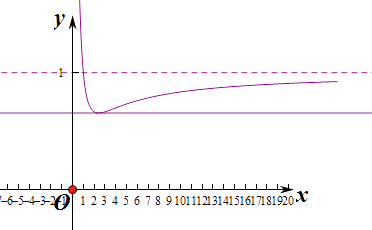
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

【题目】2015男篮亚锦赛决赛阶段,中国男篮以![]() 连胜的不败成绩赢得第
连胜的不败成绩赢得第![]() 届亚锦赛冠军,同时拿到亚洲唯一
届亚锦赛冠军,同时拿到亚洲唯一![]() 张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛
张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛![]() (最有价值球员),下表是易建联在这
(最有价值球员),下表是易建联在这![]() 场比赛中投篮的统计数据.
场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
![]()
(1)从上述![]() 场比赛中随机选择一场,求易建联在该场比赛中
场比赛中随机选择一场,求易建联在该场比赛中![]() 超过
超过![]() 的概率;
的概率;
(2)我们把比分分差不超过![]() 分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中
分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中![]() 至少有一场超过
至少有一场超过![]() 的概率;
的概率;
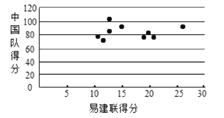
(3)用![]() 来表示易建联某场的得分,用
来表示易建联某场的得分,用![]() 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断![]() 与
与![]() 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.