题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:函数
满足:函数![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时
时![]() 是函数
是函数![]() 的导函数)成立.若
的导函数)成立.若![]() ,则
,则![]() 的大小关系是
的大小关系是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】![]() 函数
函数![]() 的图象关于直线
的图象关于直线![]() 对称,向左平移一个单位后得到函数
对称,向左平移一个单位后得到函数![]() 的图象,
的图象, ![]() 关于
关于![]() 轴对称,
轴对称, ![]() 为偶函数,
为偶函数, ![]() 函数
函数![]() 为奇函数,
为奇函数, ![]() ,
, ![]() 当
当![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,函数
时,函数![]() 上单调递减,
上单调递减, ![]() ,
, ![]() ,
,
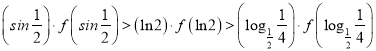 ,即
,即![]() ,故选A.
,故选A.
【方法点睛】本题主要考察抽象函数的单调性以及函数的求导法则,属于难题.求解这类问题一定要耐心读题、读懂题,通过对问题的条件和结论进行类比、联想、抽象、概括,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点也是难点就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.本题通过观察四个选项,联想到函数![]() ,再结合条件判断出其单调性,进而得出正确结论.
,再结合条件判断出其单调性,进而得出正确结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目