题目内容
【题目】已知函数f（x）= 
（x＞0）．
（1）试判断函数f（x）在（0，+∞）上单调性并证明你的结论；
（2）若f（x）＞ 
恒成立，求整数k的最大值；
（3）求证：（1+1×2）（1+2×3）…[1+n（n+1）]＞e2n﹣3 ．
【答案】
（1）解：∵f（x）= 
（x＞0），
∴f′（x）= 
[ 
]= 
[ 
]
∵x＞0，∴x2＞0， 
，ln（x+1）＞0，∴f′（x）＜0，
∴函数f（x）在（0，+∞）上是减函数
（2）解：f（x）＞ 
恒成立，即h（x）= 
＞k恒成立，
即h（x）的最小值大于k．
而h′（x）= 
，令g（x）=x﹣1﹣ln（x+1）（x＞0），
则g′（x）= ，∴g（x）在（0，+∞）上单调递增，
又g（2）=1﹣ln3＜0，g（3）=2﹣2ln2＞0，
∴g（x）=0存在唯一实根a，且满足a∈（2，3），a=1+ln（a+1）
当x＞a时，g（x）＞0，h′（x）＞0，当0＜x＜a时，g（x）＜0，h′（x）＜0，
∴h（x）min=h（a）= 
=a+1∈（3，4）
故正整数k的最大值是3
（3）证明：由（Ⅱ）知 
（x＞0）
∴ln（x+1）＞ 
﹣1=2﹣ 
＞2﹣ 
令x=n（n+1）（n∈N*），则ln[1+n（n+1）]＞2﹣ 
，
∴ln（1+1×2）+ln（1+2×3）+…+ln[1+n（n+1）]
＞（2﹣ 
）+（2﹣ 
）+…+[2﹣ ]
=2n﹣3[ 
]
=2n﹣3（1﹣ 
）=2n﹣3+ 
＞2n﹣3
∴（1+1×2）（1+2×3）…[1+n（n+1）]＞e2n﹣3
【解析】（1）对函数f（x）求导数，可判f′（x）＜0，进而可得单调性；（2）问题转化为h（x）= ＞k恒成立，通过构造函数可得h（x）min∈（3，4），进而可得k值；（3）由（2）知 
（x＞0），可得ln（x+1）＞2﹣ ，令x=n（n+1）（n∈N*），一系列式子相加，由裂项相消法可得ln（1+1×2）+ln（1+2×3）+…+ln[1+n（n+1）]＞2n﹣3，进而可得答案．
【考点精析】利用利用导数研究函数的单调性和数列的前n项和对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；数列{an}的前n项和sn与通项an的关系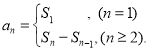
．
