题目内容
【题目】已知函数f（t）= 
，g（x）=cosxf（sinx）﹣sinxf（cosx），x∈（π， 
）．
（1）求函数g（x）的值域；
（2）若函数y=|cos（ωx+ 
）|f（sin（ωx+ ））（ω＞0）在区间[ 
，π]上为增函数，求实数ω的取值范围．
【答案】
（1）解： 
，∵ 
∴ 
，∴cosxf（sinx）=﹣1﹣sinx
同理sinxf（cosx）=﹣1﹣cosx，∴ 
∵ ，∴ 
，∴ 
∴ 
（2）解：由（1）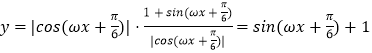 
∵ 
， 
，∴ 
令 
，k∈Z；解之得 
，k∈Z
则y=|cos（ωx+ 
）|f（sin（ωx+ ））（ω＞0）的单调递增区间为 
，k∈Z，
由已知函数y=|cos（ωx+ ）|f（sin（ωx+ ））（ω＞0）在区间[ 
，π]上为增函数，
解之得 
，
∵ ，∴k=0，∴ 
【解析】（1）求出函数g（x），利用辅助角公式化简，即可求函数g（x）的值域；（2）求出y=|cos（ωx+ ）|f（sin（ωx+ ））（ω＞0）的单调递增区间为 ，k∈Z，利用函数y=|cos（ωx+ ）|f（sin（ωx+ ））（ω＞0）在区间[ ，π]上为增函数，求实数ω的取值范围．
练习册系列答案
相关题目
