题目内容

5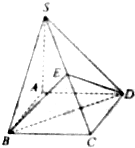．如图，四棱锥S-ABCD中底面ABCD是正方形，AS⊥底面ABCD，且AS=AB，E是SC的中点，求证：平面BDE⊥平面ABCD．

分析 根据面面垂直的判定定理即可证明平面BDE⊥平面ABCD．

解答 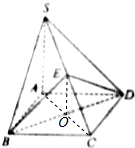证明：连结AC交BD于O，连结OE．
则OE是△SAC的中位线，
则OE∥SA，
∵AS⊥底面ABCD，
∴OE⊥平面ABCD，
∵OE?平面BDE，
∴平面BDE⊥平面ABCD．

点评 本题考查空间平面与平面的位置关系：垂直．考查平面与平面垂直的判定定理的运用，考查空间想象能力，属于中档题．

练习册系列答案
相关题目
15．已知甲、乙两人在一次射击中命中目标的概率分别为$\frac{2}{3}$和$\frac{3}{4}$，假设两人射击相互独立，且每人各次射击互不影响．
（Ⅰ）若甲、乙两人各射击1次，求至少有一个命中目标的概率；
（Ⅱ）若甲、乙两人各射击4次，求甲命中目标2次，且乙命中目标3次的概率．
16．已知函数f（x）=$\sqrt{3}$sin（ωx+φ）+2sin2$\frac{ωx+φ}{2}$-1（ω＞0，0＜φ＜π），相邻两对称轴间的距离为$\frac{π}{2}$，且f（0）=0
（1）求f（x）的解析式；
（2）将函数y=f（x）的图象沿x轴方向向右平移$\frac{π}{6}$个单位长度，再把横坐标缩短到原来的$\frac{1}{2}$（纵坐标不变），得到函数y=g（x）的图象．当x∈[-$\frac{π}{12}，\frac{π}{6}$]时，求函数g（x）的值域．
13．已知数列{an}的前n项和Sn满足：Sn=$\frac{a}{a-1}$（an-1）（a为常数，且a≠0，a≠1）．
（1）求{an}的通项公式；
（2）bn=$\frac{2{S}_{n}}{{a}_{n}}$+1，若数列{bn}为等比数列，求a的值；
（3）在（2）的条件下，设数列{2-lgbn}的前n项和为Tn，问：n为何值时，Tn最大？并求出Tn的最大值．
20．求证：1+$\frac{1}{3^2}$+$\frac{1}{5^2}$+…+$\frac{1}{（2n-1）^2}$＞$\frac{7}{6}$-$\frac{1}{2（2n+1）}$．
10．已知0＜m＜1，设a=logm（m2+1），b=logm（m+1），c=logm（2m），则a，b，c的大小关系是（　　）
A．c＞a＞bB．a＞c＞bC．a＞b＞cD．b＞a＞c
17．极坐标中，椭圆C的中心在极点O，短轴端点为P（1，$\frac{π}{2}$），一个焦点为F（$\sqrt{3}$，0）．
（1）写出椭圆C的极坐标方程；
（2）点A、B在椭圆上，且OA⊥OB，求△AOB面积的最小值．
14．化简：$\sqrt{2}$sin（$\frac{π}{4}$-x）+$\sqrt{6}$cos（$\frac{π}{4}$-x）
15．若复数z满足3z+$\overline z$=1+i，其中i是虚数单位，则z=$\frac{1}{4}+\frac{1}{2}i$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网