题目内容
20.求证:1+$\frac{1}{3^2}$+$\frac{1}{5^2}$+…+$\frac{1}{(2n-1)^2}$>$\frac{7}{6}$-$\frac{1}{2(2n+1)}$.分析 由$\frac{1}{(2n-1)^{2}}>\frac{1}{(2n-1)(2n+1)}$把不等式左边缩小,然后利用裂项相消法求和得答案.
解答 证明:1+$\frac{1}{3^2}$+$\frac{1}{5^2}$+…+$\frac{1}{(2n-1)^2}$>$1+\frac{1}{3×5}+\frac{1}{5×7}+…+\frac{1}{(2n-1)(2n+1)}$
=1+$\frac{1}{2}(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$
=1+$\frac{1}{2}(\frac{1}{3}-\frac{1}{2n+1})$=$\frac{7}{6}-\frac{1}{2(2n+1)}$.
点评 本题考查了放缩法证明数列不等式,考查了裂项相消法求数列的和,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
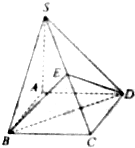 如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.
如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.