题目内容
15.已知甲、乙两人在一次射击中命中目标的概率分别为$\frac{2}{3}$和$\frac{3}{4}$,假设两人射击相互独立,且每人各次射击互不影响.(Ⅰ)若甲、乙两人各射击1次,求至少有一个命中目标的概率;
(Ⅱ)若甲、乙两人各射击4次,求甲命中目标2次,且乙命中目标3次的概率.
分析 (Ⅰ)由条件利用相互独立事件的概率乘法公式求得他们都没有击中目标的概率,再用1减去此概率的值,即为所求.
(Ⅱ)由条件根据n次独立重复试验中恰好发生k次的概率公式,求得甲命中目标2次,且乙命中目标3次的概率.
解答 解:(Ⅰ)若甲、乙两人各射击1次,由题意可得他们都没有击中目标的概率为(1-$\frac{2}{3}$)•(1-$\frac{3}{4}$)=$\frac{1}{12}$,
故至少有一个命中目标的概率为1-$\frac{1}{12}$=$\frac{11}{12}$.
(Ⅱ)若甲、乙两人各射击4次,则甲命中目标2次,且乙命中目标3次的概率为${C}_{4}^{2}$•${(\frac{2}{3})}^{2}$•${(1-\frac{2}{3})}^{2}$•${C}_{4}^{3}$•${(\frac{3}{4})}^{3}$•(1-$\frac{3}{4}$)=$\frac{1}{8}$.
点评 本题主要考查相互独立事件的概率乘法公式,以及n次独立重复试验中恰好发生k次的概率公式,事件和它的对立事件概率之间的关系,属于基础题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.定义在(0,+∞)的函数f(x)为单调函数,对任意的x∈(0,+∞)恒有f[f(x)-log4x]=5.x0是方程f(x)-f′(x)=4的一个根,则x0所在区间为( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
3.在空间中,设直线l的方向向量为$\overrightarrow{a}$,平面α的法向量为$\overrightarrow{b}$,对于原命题“若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则l∥α”,下列判断正确的是( )
| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
7.抛物线y2=4x的焦点为F,原点为O,直线AB经过点F且与抛物线交于A,B两点,抛物线的准线与x轴交于点C,若∠OFA=135°,则tan∠ACB=( )
| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
4.抛物线x2=4y的焦点到准线的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |

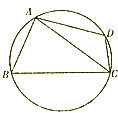 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.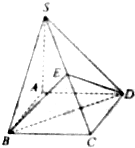 如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.
如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.