题目内容
14.化简:$\sqrt{2}$sin($\frac{π}{4}$-x)+$\sqrt{6}$cos($\frac{π}{4}$-x)分析 由题意凑出两角差的余弦公式的性质可得.
解答 解:由三角函数公式可得$\sqrt{2}$sin($\frac{π}{4}$-x)+$\sqrt{6}$cos($\frac{π}{4}$-x)
=2$\sqrt{2}$[$\frac{1}{2}$sin($\frac{π}{4}$-x)+$\frac{\sqrt{3}}{2}$cos($\frac{π}{4}$-x)]
=2$\sqrt{2}$[sin$\frac{π}{6}$sin($\frac{π}{4}$-x)+cos$\frac{π}{6}$cos($\frac{π}{4}$-x)]
=2$\sqrt{2}$cos($\frac{π}{6}$-$\frac{π}{4}$+x)
=2$\sqrt{2}$cos(x-$\frac{π}{12}$)
点评 本题考查两角和与差的正余弦函数公式,属基础题.

练习册系列答案
相关题目
4.抛物线x2=4y的焦点到准线的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
19.已知平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,y),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则y=( )
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |
14.已知平面α,β,直线m,n,下列命题中不正确的是( )
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
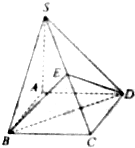 如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.
如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.