题目内容
15.若复数z满足3z+$\overline z$=1+i,其中i是虚数单位,则z=$\frac{1}{4}+\frac{1}{2}i$.分析 设z=a+bi,则$\overline{z}$=a-bi(a,b∈R),利用复数的运算法则、复数相等即可得出.
解答 解:设z=a+bi,则$\overline{z}$=a-bi(a,b∈R),
又3z+$\overline z$=1+i,
∴3(a+bi)+(a-bi)=1+i,
化为4a+2bi=1+i,
∴4a=1,2b=1,
解得a=$\frac{1}{4}$,b=$\frac{1}{2}$.
∴z=$\frac{1}{4}+\frac{1}{2}i$.
故答案为:$\frac{1}{4}+\frac{1}{2}i$.
点评 本题考查了复数的运算法则、复数相等,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知平面α,β,直线m,n,下列命题中不正确的是( )
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
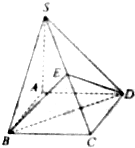 如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.
如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.