题目内容
13.已知数列{an}的前n项和Sn满足:Sn=$\frac{a}{a-1}$(an-1)(a为常数,且a≠0,a≠1).(1)求{an}的通项公式;
(2)bn=$\frac{2{S}_{n}}{{a}_{n}}$+1,若数列{bn}为等比数列,求a的值;
(3)在(2)的条件下,设数列{2-lgbn}的前n项和为Tn,问:n为何值时,Tn最大?并求出Tn的最大值.
分析 (1)由Sn=$\frac{a}{a-1}$(an-1)(a为常数,且a≠0,a≠1).知Sn+1=$\frac{a}{a-1}$(an+1-1)(a为常数,且a≠0,a≠1),利用迭代法能求出an=an
(2)得出bn=$\frac{2{S}_{n}}{{a}_{n}}$+1=$\frac{3a-1}{a-1}$$-\frac{2}{a-1}$•a1-n,根据等比数列的通项公式的特点得出必需满足$\frac{3a-1}{a-1}$=0,即可求解a的值.
(3)Cn=2-lgbn=2-nlg3,可判断{Cn}为等差数列,根据数列的性质得出c6>0,c7<0,可判断当n=6时,T6最大,求解即可得出Tn的值.
解答 解:(1)∵Sn=$\frac{a}{a-1}$(an-1)(a为常数,且a≠0,a≠1).
∴Sn+1=$\frac{a}{a-1}$(an+1-1),
从而an+1=Sn+1-Sn=$\frac{a}{a-1}$(an+1-an),
∴an+1=a•an,
当n=1时,由Sn=$\frac{a}{a-1}$(an-1),得a1=a.
∴数列{an}是以a为首项,a为公比的等比数列,故an=an.
(2)∵an=an,Sn=$\frac{a}{a-1}$(an-1)(a为常数,且a≠0,a≠1).
∴bn=$\frac{2{S}_{n}}{{a}_{n}}$+1=$\frac{3a-1}{a-1}$$-\frac{2}{a-1}$•a1-n,
∵数列{bn}为等比数列,
∴$\frac{{b}_{n+1}}{{b}_{n}}$=常数,
必需满足$\frac{3a-1}{a-1}$=0,即a=$\frac{1}{3}$.
(3)根据(2)得出bn=3n,
∴Cn=2-lgbn=2-nlg3,可判断{Cn}为等差数列,公差为-lg3,单调递减数列.
数列{2-lgbn}的前n项和为Tn=$\frac{n(4-(n+1)lg3)}{2}$
c6=2-6×lg3>0,c7=2-7×lg3<0,
可知:当n=6时,T6最大为$\frac{6×[4-7lg3]}{2}$=12-21lg3
点评 本题考查数列的通项公式的应用,考查数列前n项和的求法,解题时要认真审题,注意迭代法和错位相减法的灵活运用,利用等差数列的性质,不等式求解即可解决问题.

| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
| A. | x2=8y | B. | x2=10y | C. | x2=9y | D. | x2=5y |
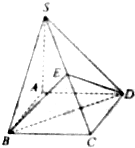 如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.
如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.