题目内容
17.极坐标中,椭圆C的中心在极点O,短轴端点为P(1,$\frac{π}{2}$),一个焦点为F($\sqrt{3}$,0).(1)写出椭圆C的极坐标方程;
(2)点A、B在椭圆上,且OA⊥OB,求△AOB面积的最小值.
分析 (1)利用椭圆的短轴端点为P(1,$\frac{π}{2}$),一个焦点为F($\sqrt{3}$,0),可得b=1,c=$\sqrt{3}$,a=2,求出椭圆的直角坐标方程,再求出椭圆C的极坐标方程;
(2)设出A,B的坐标,代入椭圆方程,两式相加,利用基本不等式求出△OAB面积的最小值.
解答 解:(1)椭圆的短轴端点为P(1,$\frac{π}{2}$),一个焦点为F($\sqrt{3}$,0).
所以b=1,c=$\sqrt{3}$,
所以a=2,
所以椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$,
所以椭圆C的极坐标方程为ρ2cos2α+4ρ2sin2α=4;
(2)可由OA⊥OB,设A(|OA|cosα,|OA|sinα),B(|OB|cos(α+$\frac{π}{2}$),|OB|sin(α+$\frac{π}{2}$)),即B(-|OB|sinα,|OB|cosα).
将A,B代入椭圆方程后可得:$\frac{co{s}^{2}α}{4}+si{n}^{2}α$=$\frac{1}{|OA{|}^{2}}$,$\frac{si{n}^{2}α}{4}+co{s}^{2}α$=$\frac{1}{|OB{|}^{2}}$
两式相加可得:$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{5}{4}$
同时:$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$≥$\frac{2}{|OA||OB|}$,
所以|OA||OB|≥$\frac{8}{5}$,
所以S△OAB=$\frac{1}{2}$|OA||OB|≥$\frac{4}{5}$,当且仅当|OA|=|OB|时取等,即△OAB面积的最小值为$\frac{4}{5}$. (12分)
点评 本题考查椭圆的方程与性质,考查椭圆的参数方程,考查直线与圆的位置关系,考查基本不等式的运用,确定椭圆的方程是关键.

| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
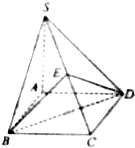 如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.
如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.