题目内容
16.已知函数f(x)=$\sqrt{3}$sin(ωx+φ)+2sin2$\frac{ωx+φ}{2}$-1(ω>0,0<φ<π),相邻两对称轴间的距离为$\frac{π}{2}$,且f(0)=0(1)求f(x)的解析式;
(2)将函数y=f(x)的图象沿x轴方向向右平移$\frac{π}{6}$个单位长度,再把横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),得到函数y=g(x)的图象.当x∈[-$\frac{π}{12},\frac{π}{6}$]时,求函数g(x)的值域.
分析 (1)化简可得f(x)=2sin(ωx+φ-$\frac{π}{6}$),由题意可得ω和φ值,可得解析式;
(2)由图象变换可得g(x)=2sin(4x-$\frac{π}{3}$),由x∈[-$\frac{π}{12},\frac{π}{6}$]和三角函数的性质可得值域.
解答 解:(1)化简可得f(x)=$\sqrt{3}$sin(ωx+φ)+2sin2$\frac{ωx+φ}{2}$-1
=$\sqrt{3}$sin(ωx+φ)-cos(ωx+φ)=2sin(ωx+φ-$\frac{π}{6}$)
∵相邻两对称轴间的距离为$\frac{π}{2}$,∴$\frac{2π}{2ω}$=$\frac{π}{2}$,解得ω=2,
∴f(x)=2sin(2x+φ-$\frac{π}{6}$),
∵f(0)=0,0<φ<π,∴φ=$\frac{π}{6}$
∴f(x)=2sin(2x);
(2)函数y=f(x)的图象沿x轴方向向右平移$\frac{π}{6}$个单位长度,的函数y=2sin(2x-$\frac{π}{3}$);
再把横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),得到函数y=g(x)的图象,
∴g(x)=2sin(4x-$\frac{π}{3}$),∵x∈[-$\frac{π}{12},\frac{π}{6}$],∴4x-$\frac{π}{3}$∈[-$\frac{2π}{3}$,$\frac{π}{3}$],
∴sin(4x-$\frac{π}{3}$)∈[-1,$\frac{\sqrt{3}}{2}$],∴函数的值域为[-2,$\sqrt{3}$]
点评 本题考查三角函数图象的变换以及三角函数图象和性质,属基础题.

练习册系列答案
相关题目
6.定义在(0,+∞)的函数f(x)为单调函数,对任意的x∈(0,+∞)恒有f[f(x)-log4x]=5.x0是方程f(x)-f′(x)=4的一个根,则x0所在区间为( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
7.抛物线y2=4x的焦点为F,原点为O,直线AB经过点F且与抛物线交于A,B两点,抛物线的准线与x轴交于点C,若∠OFA=135°,则tan∠ACB=( )
| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
4.抛物线x2=4y的焦点到准线的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
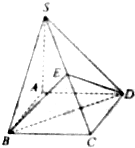 如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.
如图,四棱锥S-ABCD中底面ABCD是正方形,AS⊥底面ABCD,且AS=AB,E是SC的中点,求证:平面BDE⊥平面ABCD.