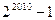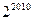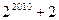题目内容
(本小题满分13分)
在数列{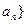 中,
中,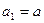 (
(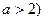 且
且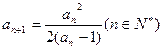
(1)求证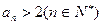 ;(2)求证
;(2)求证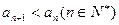 ;
;
(3)若存在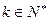 ,使得
,使得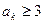 ,求证:
,求证: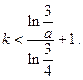
在数列{
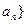 中,
中,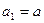 (
(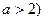 且
且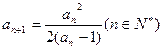
(1)求证
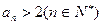 ;(2)求证
;(2)求证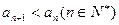 ;
;(3)若存在
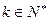 ,使得
,使得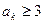 ,求证:
,求证: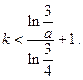
见解析
证明:(1)(解法一)1当n=1时,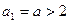 ,命题成立;…………… 1分
,命题成立;…………… 1分
2设当n=k时(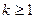 且n
且n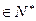 )命题成立,即
)命题成立,即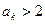
而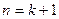 时,
时,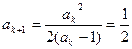 [
[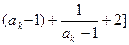
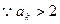 ,
,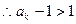 ,
,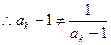 ,
,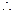
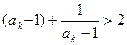
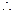
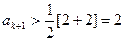 ,
,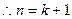 时,
时,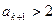 ,命题也成立
,命题也成立
由12对一切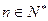 有
有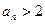 ………………………………5分
………………………………5分
(解法二)(反证法)当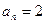 时解得
时解得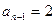 ,
,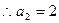 ,
,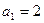 矛盾
矛盾
当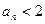 时,
时,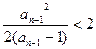 ,则
,则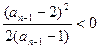
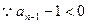 则有
则有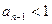 ,那么有
,那么有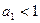 矛盾
矛盾
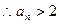 …………………………………………………………5分
…………………………………………………………5分
(2)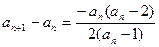
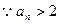 ,
,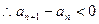 ,
,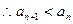 …………………………8分
…………………………8分
(3)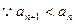 ,
,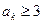
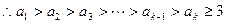
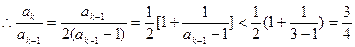
即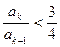
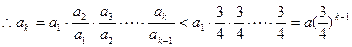
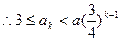 ,
,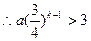 ,
,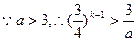
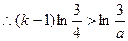 ,又
,又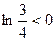
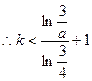 ……………………………………………………13分
……………………………………………………13分
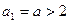 ,命题成立;…………… 1分
,命题成立;…………… 1分2设当n=k时(
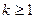 且n
且n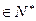 )命题成立,即
)命题成立,即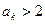
而
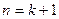 时,
时,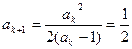 [
[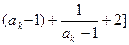
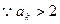 ,
,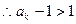 ,
,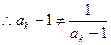 ,
,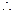
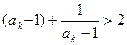
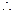
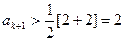 ,
,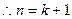 时,
时,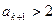 ,命题也成立
,命题也成立由12对一切
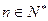 有
有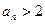 ………………………………5分
………………………………5分(解法二)(反证法)当
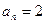 时解得
时解得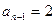 ,
,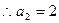 ,
,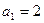 矛盾
矛盾当
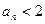 时,
时,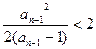 ,则
,则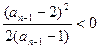
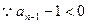 则有
则有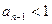 ,那么有
,那么有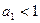 矛盾
矛盾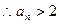 …………………………………………………………5分
…………………………………………………………5分(2)
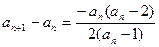
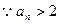 ,
,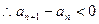 ,
,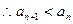 …………………………8分
…………………………8分(3)
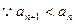 ,
,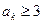
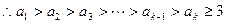
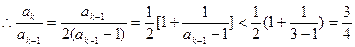
即
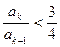
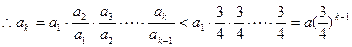
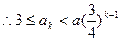 ,
,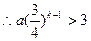 ,
,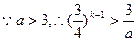
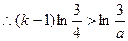 ,又
,又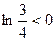
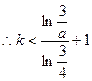 ……………………………………………………13分
……………………………………………………13分
练习册系列答案
相关题目
 为集合
为集合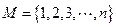 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于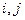 满足下列条件:
满足下列条件: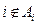 ,且每一个
,且每一个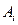 至
至 少含有三个元素;
少含有三个元素;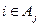 的充要条件是
的充要条件是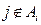 (其中
(其中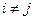 )。
)。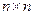 数表),规定第
数表),规定第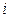 行第
行第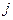 列数为:
列数为: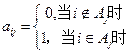 。
。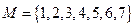 ,请完成下面
,请完成下面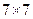 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);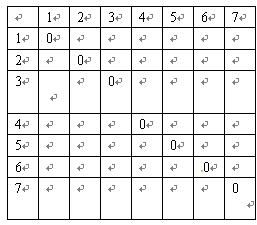
 中1的个数
中1的个数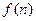 ,并证明
,并证明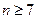 ;
;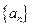 前
前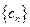 的通项公式为:
的通项公式为: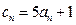 ,证明不等式:
,证明不等式: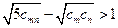 对任何正整数
对任何正整数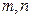 都成立。
都成立。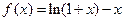 在区间
在区间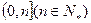 上的最小值为
上的最小值为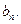 令
令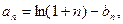
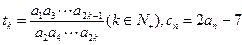 .
.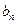 ;
;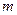 ,使得
,使得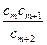 为数列
为数列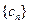 中的项;
中的项;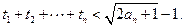
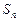 为等差数列
为等差数列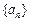 的前
的前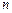 项和,且
项和,且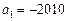 ,
,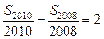 ,则
,则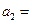 ( )
( )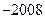
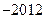
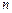 个图形包含
个图形包含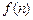 个“福娃迎迎”,
个“福娃迎迎”, ;
; ____________.(答案用数字或
____________.(答案用数字或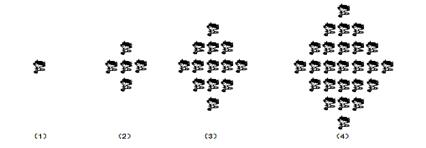
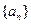 的前n项和为
的前n项和为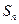 ,若
,若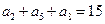 , 则
, 则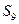 =
= ( ).
( ).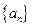 中,
中,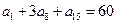 ,则
,则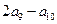 的值为
的值为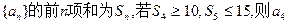 的最大值是 。
的最大值是 。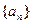 中,
中,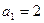 ,且
,且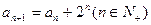 ,则
,则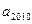 为 ( )
为 ( )