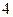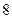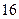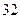题目内容
设函数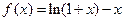 在区间
在区间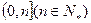 上的最小值为
上的最小值为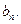 令
令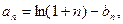
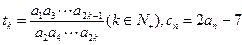 .
.
(Ⅰ)求 ;
;
(Ⅱ)试求所有的正整数 ,使得
,使得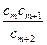 为数列
为数列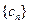 中的项;
中的项;
(Ⅲ)求证: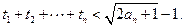
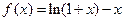 在区间
在区间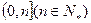 上的最小值为
上的最小值为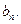 令
令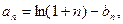
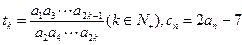 .
.(Ⅰ)求
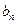 ;
;(Ⅱ)试求所有的正整数
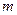 ,使得
,使得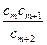 为数列
为数列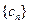 中的项;
中的项;(Ⅲ)求证:
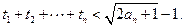
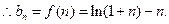 ,
,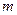 为
为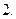
(Ⅰ)显然函数的定义域为
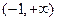
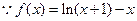 ,
,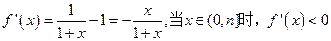
故函数
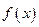 在区间
在区间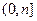 上是减函数
上是减函数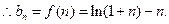
(Ⅱ)
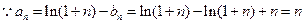
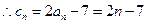
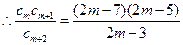 ,设
,设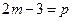 ,
, 则
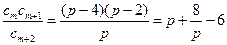 ,
, 所以
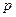 为8的约数
为8的约数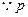 为奇数,
为奇数,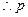 的取值可为
的取值可为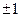
当
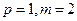 时,
时,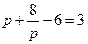 是数列
是数列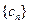 中的项
中的项当
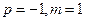 时,
时,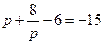 ,而数列
,而数列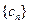 中的最小项为
中的最小项为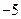 ,所以不符合
,所以不符合故满足条件的所有
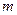 为
为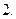
(Ⅲ)
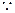
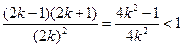
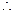
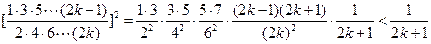
又
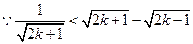
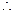
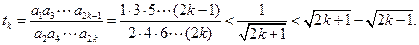

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
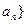 中,
中,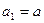 (
(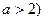 且
且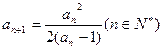
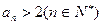 ;(2)求证
;(2)求证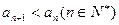 ;
;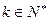 ,使得
,使得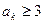 ,求证:
,求证: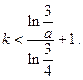
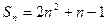 ,数列{bn}满足b1+3b2+…+(2n-1)b
,数列{bn}满足b1+3b2+…+(2n-1)b n=(2n―3)·2n+1,
n=(2n―3)·2n+1,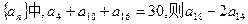 的值为 ( )
的值为 ( )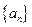 中,
中,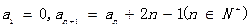 ,则数列
,则数列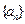 的首项
的首项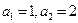 ,前
,前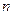 项和
项和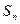 恒为正数,且当
恒为正数,且当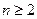 时,
时,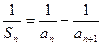 .
.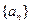 的通项公式;
的通项公式;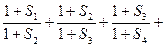
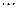
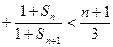 .
.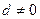 的等差数列{an}中的项组成一个新数列
的等差数列{an}中的项组成一个新数列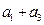 ,
, 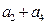 ,
,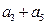 ,…,则下列说法正确的是
,…,则下列说法正确的是 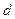 的等差数列
的等差数列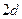 的等差数列
的等差数列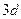 的等差数列
的等差数列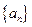 中,
中,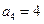 ,则
,则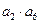 等于--------------------------------( )
等于--------------------------------( )