题目内容
(本题满分 13分)
集合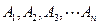 为集合
为集合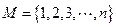 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数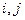 满足下列条件:
满足下列条件:
①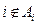 ,且每一个
,且每一个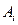 至
至 少含有三个元素;
少含有三个元素;
②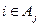 的充要条件是
的充要条件是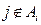 (其中
(其中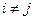 )。
)。
为了表示这些子集,作 行
行 列的数表(即
列的数表(即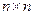 数表),规定第
数表),规定第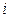 行第
行第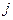 列数为:
列数为: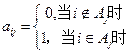 。
。
(1)该表中每一列至少有多少个1;若集合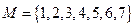 ,请完成下面
,请完成下面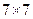 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);
(2)用含 的代数式表示
的代数式表示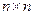 数表
数表 中1的个数
中1的个数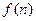 ,并证明
,并证明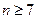 ;
;
(3)设数列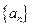 前
前 项和为
项和为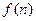 ,数列
,数列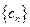 的通项公式为:
的通项公式为: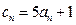 ,证明不等式:
,证明不等式: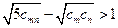 对任何正整数
对任何正整数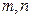 都成立。
都成立。
集合
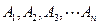 为集合
为集合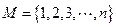 的
的 个不同的子集,对于任意不大于
个不同的子集,对于任意不大于 的正整数
的正整数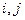 满足下列条件:
满足下列条件:①
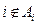 ,且每一个
,且每一个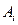 至
至 少含有三个元素;
少含有三个元素;②
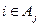 的充要条件是
的充要条件是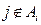 (其中
(其中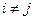 )。
)。为了表示这些子集,作
 行
行 列的数表(即
列的数表(即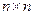 数表),规定第
数表),规定第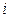 行第
行第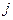 列数为:
列数为: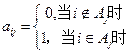 。
。(1)该表中每一列至少有多少个1;若集合
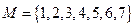 ,请完成下面
,请完成下面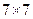 数表(填符合题意的一种即可);
数表(填符合题意的一种即可);
(2)用含
 的代数式表示
的代数式表示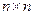 数表
数表 中1的个数
中1的个数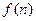 ,并证明
,并证明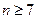 ;
;(3)设数列
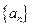 前
前 项和为
项和为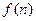 ,数列
,数列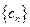 的通项公式为:
的通项公式为: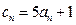 ,证明不等式:
,证明不等式: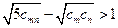 对任何正整数
对任何正整数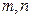 都成立。
都成立。(1)见解析。
(2) ,证明见解析。
,证明见解析。
(3)证明见解析。
(2)
 ,证明见解析。
,证明见解析。(3)证明见解析。
(1)根据条件①每个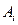 中至少含有三个元素,作出的数表每一列至少有三个1。
中至少含有三个元素,作出的数表每一列至少有三个1。
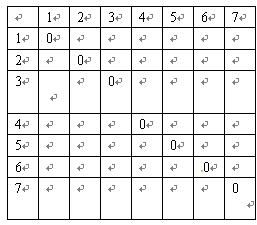
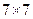 数表如下:
数表如下:
(2)题设条件①中的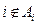 表明的一条对角线上数字都是0,题设条件②表明除对角线以外,
表明的一条对角线上数字都是0,题设条件②表明除对角线以外,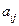 与
与 恰好一个为1,而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有
恰好一个为1,而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有 个1。另一方面,根据题设条件①每一个
个1。另一方面,根据题设条件①每一个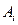 至少含有三个元素得:作出的
至少含有三个元素得:作出的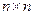 数表的每一列至少有3个1,所以整个
数表的每一列至少有3个1,所以整个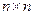 数表(共有
数表(共有 列)至少有
列)至少有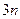 个1,因此列出不等式:
个1,因此列出不等式: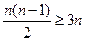 ,解得
,解得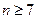 。
。
(3)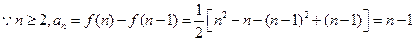
检验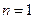 也成立,故
也成立,故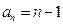
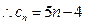
证法一:要证: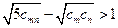 ,只要证:
,只要证: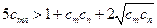
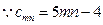 ,
,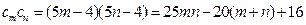
故只要证: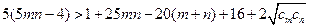 ,
,
即只要证 :
: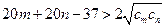 , 又
, 又
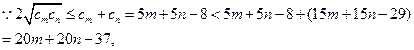
所以命题得证。
证法二:同上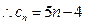
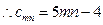 又
又

所以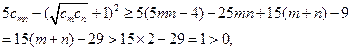
即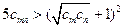 ,故
,故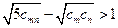
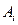 中至少含有三个元素,作出的数表每一列至少有三个1。
中至少含有三个元素,作出的数表每一列至少有三个1。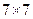 数表如下:
数表如下:| | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
 3 3 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 6 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
(2)题设条件①中的
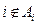 表明的一条对角线上数字都是0,题设条件②表明除对角线以外,
表明的一条对角线上数字都是0,题设条件②表明除对角线以外,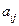 与
与 恰好一个为1,而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有
恰好一个为1,而另一个为0,即数表中除该对角线以外,0与1各占一半,故数表中共有 个1。另一方面,根据题设条件①每一个
个1。另一方面,根据题设条件①每一个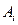 至少含有三个元素得:作出的
至少含有三个元素得:作出的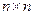 数表的每一列至少有3个1,所以整个
数表的每一列至少有3个1,所以整个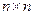 数表(共有
数表(共有 列)至少有
列)至少有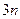 个1,因此列出不等式:
个1,因此列出不等式: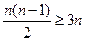 ,解得
,解得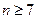 。
。(3)
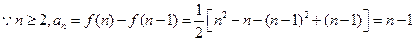
检验
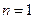 也成立,故
也成立,故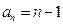
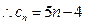
证法一:要证:
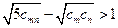 ,只要证:
,只要证: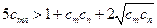
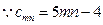 ,
,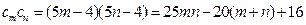
故只要证:
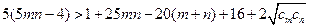 ,
,即只要证
 :
: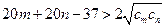 , 又
, 又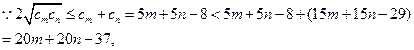
所以命题得证。
证法二:同上
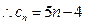
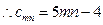 又
又
所以
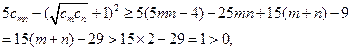
即
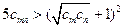 ,故
,故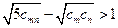

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
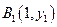 、
、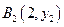 、…、
、…、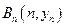 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数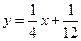 图像上的点,点列
图像上的点,点列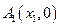 、
、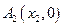 、…、
、…、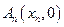 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中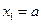 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点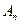 、
、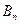 、
、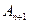 构成一个顶角的顶点为
构成一个顶角的顶点为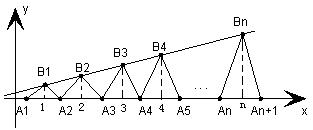
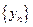 的通项公式,并证明
的通项公式,并证明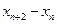 为常数,并求出数列
为常数,并求出数列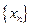 的通项公式;
的通项公式;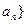 中,
中,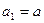 (
(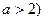 且
且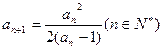
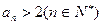 ;(2)求证
;(2)求证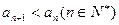 ;
;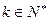 ,使得
,使得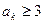 ,求证:
,求证: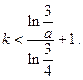
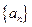 的前n项积为
的前n项积为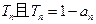 ;数列
;数列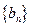 的前n项和为
的前n项和为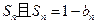 .
.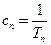 .①证明数列
.①证明数列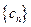 成等差数列;②求证数列
成等差数列;②求证数列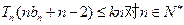 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.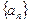 中,已知
中,已知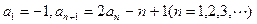
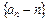 是等比数列
是等比数列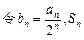 为数列
为数列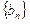 的前
的前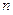 项和,求
项和,求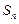 的表达式
的表达式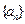 的首项
的首项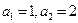 ,前
,前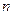 项和
项和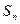 恒为正数,且当
恒为正数,且当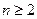 时,
时,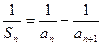 .
.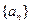 的通项公式;
的通项公式;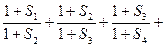
 .
. 中,
中, ,则
,则 的值为
的值为 中,
中,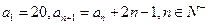 则数列
则数列