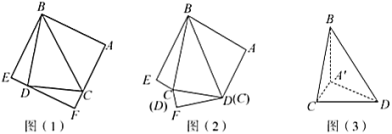
题目内容
【题目】如图(1),边长为![]() 的正方形
的正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,现沿
,现沿![]() 把
把![]() 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将![]() ,
,![]() ,
,![]() 沿
沿![]() ,
,![]() ,
,![]() 折起,使
折起,使![]() 、
、![]() 、
、![]() 三点重合于点
三点重合于点![]() ,如图(3).
,如图(3).
(1)求证:![]() ;
;
(2)求二面角![]() 最小时的余弦值.
最小时的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用图形翻折的几何关系可得出![]() ,
,![]() ,然后由直线与平面垂直的判定定理可得出
,然后由直线与平面垂直的判定定理可得出![]() 平面
平面![]() ,由此可证明出
,由此可证明出![]() ;
;
(2)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,令
轴建立空间直角坐标系,令![]() ,
,![]() ,可得出
,可得出![]() ,求出平面
,求出平面![]() 和平面
和平面![]() 的法向量,然后利用空间向量法结合基本不等式可求出二面角
的法向量,然后利用空间向量法结合基本不等式可求出二面角![]() 最小时的余弦值.
最小时的余弦值.
(1)折叠前![]() ,
,![]() ,折叠后
,折叠后![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,因此
,因此![]() ;
;
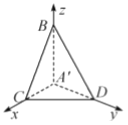
(2)由(1)及题意知![]() ,因此以
,因此以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别
分别
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系如图:
轴建立空间直角坐标系如图:
令![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]()
设平面![]() 法向量为
法向量为![]()
则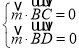 所以
所以![]() ,令
,令![]() ,则
,则![]()
又平面![]() 法向量为
法向量为![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,所以
,所以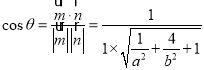 ,
,
又![]() ,
,
当且仅当![]() 取等号,所以
取等号,所以![]() .
.
所以二面角![]() 最小时的余弦值为
最小时的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】由于工作需要,某公司准备一次性购买两台具有智能打印、扫描、复印等多种功能的智能激光型打印机.针对购买后未来五年内的售后,厂家提供如下两种方案:
方案一:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元;
元;
方案二:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元.
元.
该公司搜集并整理了![]() 台这款打印机使用五年的维修次数,所得数据如下表所示:
台这款打印机使用五年的维修次数,所得数据如下表所示:
维修次数 |
|
|
|
|
台数 |
|
|
|
|
以这![]() 台打印机使用五年的维修次数的频率代替
台打印机使用五年的维修次数的频率代替![]() 台打印机使用五年的维修次数的概率,记
台打印机使用五年的维修次数的概率,记![]() 表示这两台智能打印机五年内共需维修的次数.
表示这两台智能打印机五年内共需维修的次数.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以两种方案产生的维修费用的期望值为决策依据,写出你的选择,并说明理由.