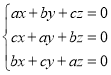题目内容
【题目】已知函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)在曲线![]() 上是否存在点P,使得过点P可作三条直线与曲线
上是否存在点P,使得过点P可作三条直线与曲线![]() 相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
相切?若存在,求出其横坐标的取值范围;若不存在,请说明理由.
【答案】(1)当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ;(2)存在,
;(2)存在, .
.
【解析】
(1)求出导数![]() ,确定函数的单调性,然后按
,确定函数的单调性,然后按![]() 分类讨论;
分类讨论;
(2)假设存在符合条件的点![]() ,同时设切点为
,同时设切点为![]() ,由导数几何意义得
,由导数几何意义得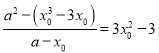 即
即![]() (*),问题转化为关于
(*),问题转化为关于![]() 的方程(*)存在三个不同实根.然后用导数研究函数
的方程(*)存在三个不同实根.然后用导数研究函数![]() 的零点.
的零点.
(1)由题意得:![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
即![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
又![]() 的零点分别为
的零点分别为![]() ,0,
,0,![]()
所以当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() .
.
(2)假设存在符合条件的点![]() ,切点设为
,切点设为![]()
所以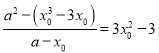 即
即![]() (*)
(*)
故问题转化为关于![]() 的方程(*)存在三个不同实根.
的方程(*)存在三个不同实根.
令![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 在R上单调递增,不合题意;
在R上单调递增,不合题意;
当![]() 时,易知
时,易知![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
从而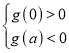 ,即
,即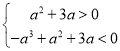
解得:![]()
当![]() 时,易知
时,易知![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
从而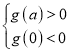 ,即
,即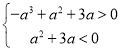
解得:![]()
综上,存在符合条件的点P,其横坐标的取值范围为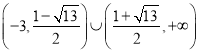 .
.

【题目】端午节是中国传统节日之一节日期间,各大商场各种品牌的“粽子战”便悄然打响.某记者走访市场发现,各大商场粽子种类繁多,价格不一根据数据统计分析,得到了某商场不同种类的粽子销售价格(单位:元/千克)的频数分布表,如表一所示.
表一:
价格/(元/千克) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) |
种类数 | 4 | 12 | 16 | 6 | 2 |
在调查中,记者还发现,各大品牌在馅料方面还做足了功课,满足了市民多样化的需求除了蜜枣、豆沙等传统馅料粽,很多品牌还推出了鲜肉、巧克力、海鲜等特色馅料粽在该商场内,记者随机对100名顾客的年龄和粽子口味偏好进行了调查,结果如表二.
表二:
喜欢传统馅料粽 | 喜欢特色馅料粽 | 总计 | |
40岁以下 | 30 | 15 | 45 |
40岁及以上 | 50 | 5 | 55 |
总计 | 80 | 20 | 100 |
(1)根据表一估计该商场粽子的平均销售价(同一组中的数据用该组区间的中点值代表);
(2)根据表二信息能否有95%的把握认为顾客的粽子口味偏好与年龄有关?
参考公式和数据: (其中
(其中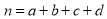 为样本容量)
为样本容量)
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |